Question

Сторона АВ треугольника АВС разделена на 3 равные части и через точки деления проведены прямые, параллельные стороне АС. Найдите площадь трапеции, заключенной между ними, если площадь треугольника равна 93.

Answer 1

решение в скане............

Answer 2

Спасибо большое!

Answer 3

Удачи Вам.

Answer 4

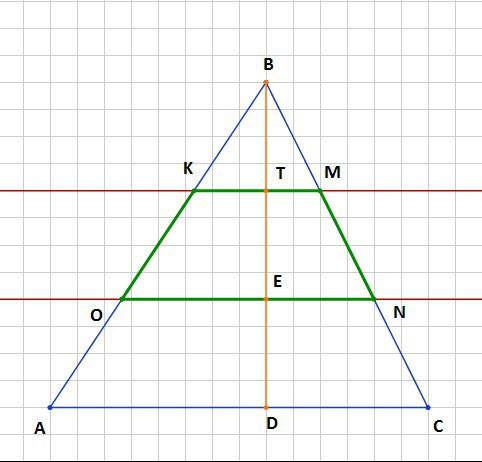
На рисунке во вложении показан треугольник АВС, разделённый на равные части по стороне АВ и получившаяся при этом разделении трапеция OKMN. ВD - высота треугольника АВС, которая разделена на три равных отрезка ВТ=ТЕ=ЕD обозначим их h, т.е. BD=BT+TE+ED=3h.
Площадь треугольника АВС:
$S_{ABC}= frac{1}{2}AC*BD$
Площадь трапеции OKMN:
$S_{OKMN}= frac{1}{2}(KM+ON)*ED$
Площадь трапеции OKMN можно найти если вычесть из площади треугольника АВС площадь треугольника KBM и площадь трапеции AONC, которые вычисляются по формулам
$S_{KBM}= frac{1}{2}KM*BT$
$S_{AONC}= frac{1}{2}(ON+AC)*ED$
$S_{OKMN}=S_{ABC}-S_{KBM}-S_{AONC}$
$frac{1}{2}(KM+ON)*BT= frac{1}{2}AC*BD- frac{1}{2}KM*BT- frac{1}{2}(ON+AC)*ED$
$frac{1}{2}(KM+ON)*h= frac{1}{2}AC*3h- frac{1}{2}KM*h- frac{1}{2}ON*h- frac{1}{2} AC*h$
$frac{1}{2}(KM+ON)*h= frac{1}{2}AC*3h- frac{1}{2}h(KM+ON)- frac{1}{2} AC*h$
$frac{1}{2}h(KM+ON)+frac{1}{2}h(KM+ON)= frac{3}{2}AC*h- frac{1}{2} AC*h$
$h(KM+ON)=AC*h$
$AC=KM+ON$
Подставляем найденное значение АС в формулу площади треугольника АВС
$S_{ABC}= frac{1}{2}(KM+ON)*3h$
$frac{1}{2}(KM+ON)*h= frac{S_{ABC}}{3}= frac{93}{3}=31$

Ответ: площадь трапеции равна 31

Answer 5

Спасибо большое!