Question

Решите уравнение
$displaystyle sin x=left|frac{3x}{2pi}-frac{3}{4}right|$

Answer 1

Функция у=sinx - ограничена,
-1≤ sinx ≤1

Функция $y=| frac{3x}{2 pi } - frac{3}{4} |$ принимает только неотрицательные значения.
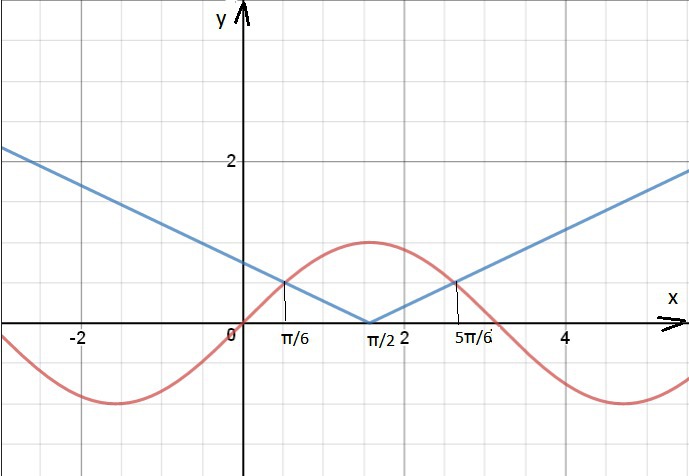
у=0    при (3х/2π)-(3/4)=0  ⇒  х=π/2
на(-∞;π/2) функция убывает и имеет одну точку пересечения с графиком у=sinx, это х=π/6.
Проверяем
sin(π/6)=|1/4 - 3/4| - верно, так как
1/2=|-2/4|
на(π/2;+∞) функция возрастает  и имеет одну точку пересечения с графиком у=sinx, это х=5π/6.
Проверяем
sin(5π/6)=|5/4 - 3/4| - верно, так как
1/2=|2/4|.
Других точек пересечения графиков нет.
О т в е т. π/6; 5π/6.

Answer 2

в коментарях написано, НЕ графически

Answer 3

Это нестандартное уравнение. Поэтому решение с опорой на графики. Проверка. Подбор.

Answer 4

на(-∞;π/2) функция убывает и имеет одну точку пересечения с графиком у=sinx, это х=π/6. Как определить, что одну точку?

Answer 5

На {π/2;π/2} у=sinx монотонно возрастает и принимает значения {-1;1]. Функция у=| (3х/2π)-(3/4)| на этом же интервале монотонно убывает и принимает значения [1,5;0]. Есть теорема, что монотонно возрастающая и монотонно убывающая функция пересекутся только в одной точке. На (--∞;-π/2) у=| (3х/2π)-(3/4)| принимает значения больше 1,5 и не имеет точек пересечения с у=sinx.