Предмет: Алгебра,
автор: Неуловимыйтип
Исследуйте функцию у = f(x) на чётность:

Ответы
Автор ответа:
0
Функция четная.
Функция четная
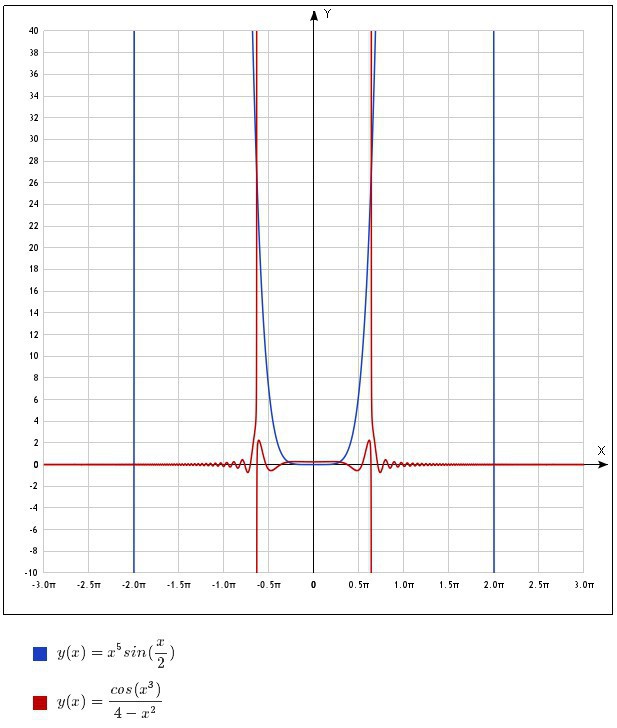
Во вложении даны графики обоих функций. Можно убедиться, что они симметричны относительно вертикальной оси, т.е. функции действительно четные.
Приложения:
Автор ответа:
0
wolframalpha использовал?
Автор ответа:
0
Для графиков? Нет y(x), а уж что он использует - это их дело.
Похожие вопросы
Предмет: Українська мова,
автор: kokoreva260276
Предмет: Математика,
автор: Russia58Girl
Предмет: Математика,
автор: mariafedunisin
Предмет: Математика,
автор: iuiiiazotova79
Предмет: Математика,
автор: defayl