У меня вообще не получается, помогите пожалуйста

Ответы
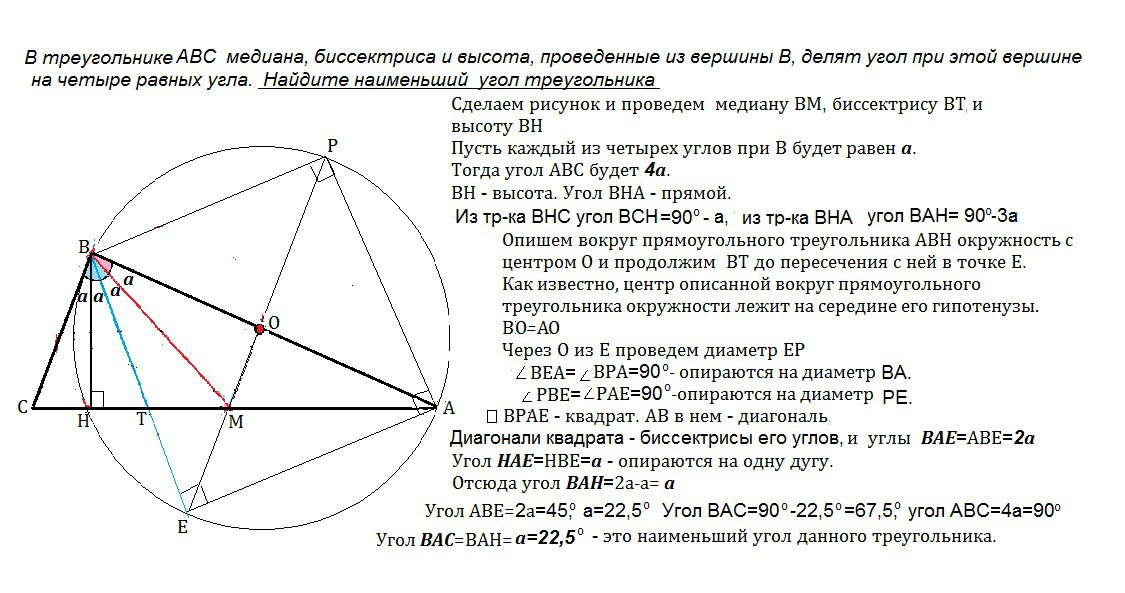
В треугольнике АВС медиана, биссектриса и высота, проведенные из вершины В, делят угол при этой вершине на четыре равных угла. Найдите наименьший угол треугольника
Сделаем рисунок и проведем медиану ВМ, биссектрису ВТ и высоту ВН
Пусть каждый из четырех углов при В будет а.
Тогда угол АВС будет 4а.
ВН - высота. Угол ВНА - прямой.
Из ⊿ ВНС угол ВСН=90º-а, из ⊿ ВНА угол ВАН=90º-3а
Опишем вокруг прямоугольного треугольника АВН окружность и продолжим ВТ до пересечения с ней в точке Е.
Через О из Е проведем диаметр ЕР
∠ ВЕА= ∠ВРА=90º - опираются на диаметр.
∠ РВЕ= ∠РАЕ=90º- опираются на диаметр. ⇒
Четырехугольник ВРАЕ - квадрат. АВ в нем - диагональ и биссектриса и делит углы РВЕ и РАЕ пополам.
∠ВАЕ=∠АВЕ=2а
Угол НАЕ=НВЕ=а - опираются на одну дугу.
Отсюда ∠ВАН=∠ВАЕ-НАЕ=2а-а=а
Т.к. диагональ квадрата является биссектрисой прямого угла, угол АВЕ=45º.
2а=45º, ⇒ а=22,5º
Угол АВС=4а=90º
Угол ВСА=90º-а=67,5º
Угол ВАС=ВАН=а=22,5º - это наименьший угол данного треугольника АВС.