Question

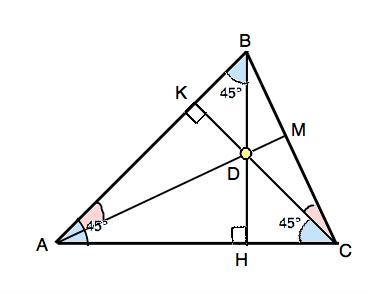
Внутри треугольника АВС взята точка D такая, что ABD = ACD = 45. Докажите, что отрезки AD и BC перпендикулярны и равны, если угол ВАС равен 45.

Answer 1

 Внутри треугольника АВС взята точка D такая, что угол ABD = угол ACD = 45°. Докажите, что отрезки AD и BC перпендикулярны и равны, если угол ВАС равен 45°

                        *   *   *

 Продлим ВD  до пересечения с АС в т.Н, а отрезок СD - до пересечения с АВ в т.К и проведем АМ через т.D.

∠АСD=45° по условию, Если ∠ВАС=45°, то  ∠АКС=90° и ∆ АСК – равнобедренный прямоугольный.  АК=СК.

  В ∆ АВН  два угла при АВ равны 45°⇒∠ВНА=90° и ∆ АВН - равнобедренный прямоугольный, Тогда точка D - пересечение высот СК и ВН треугольника АВС. Отрезок АМ, содержащий АD,  проходит через точку пересечения высот, следовательно, является высотой и перпендикулярен ВС. Отсюда АD⊥ВС. Доказано.

 Прямоугольные ⊿ АКD и ⊿ CMD подобны по равному углу при вершине   D ( вертикальные) ⇒ ∠КАD=∠MCD.

 Рассмотрим ⊿ АКD и ⊿ ВКС. Из ⊿ АКС их катеты АК=СК. Острые ∠КАD и ∠КСВ равны (из доказанного выше). Следовательно, ⊿ АКD=⊿ ВКС по катету и острому углу. Отсюда следует равенство гипотенуз этих треугольников.  АD=ВС, ч.т.д.