Question

найти наименьшее значение функции y=(x+3)в квадрате умножить на скобку (x+5)-1 на отрезке [-4,-1]

Answer 1

ДАНО
y = (x+3)² *(x-5) - 1
Преобразуем
y =(x²+6x+9)*(x-5)-1 = x³ - 5x² + 6x²-30x +9x-45-1 
y = x³+x²-21x-46
Находим производную для поиска максимума функции
у' = 3x²+2x-21
Корни квадратного уравнения  х1=-3 и х2 = 2,33
Максимальное значение при х= -3 
Минимальное значение при х=-1
у = -25
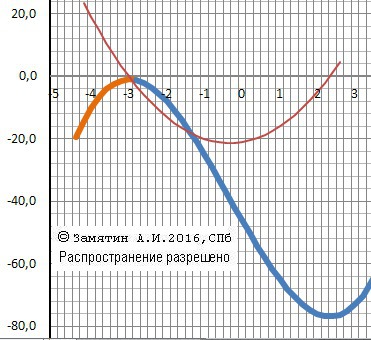
График функции на рисунке.