Предмет: Физика,
автор: maksimizgagin
В цепи со смешанным соединением сопротивлений (рисунок 4)
I1=5 A, R1=5 Ом, R2=6,25 Ом, R3=60 Ом, R4= 5 ОМ, R5=15 Ом , R6=15 Ом, Ro=0,2 Ом.
Вычислить токи, напряжения и мощности каждого участка и всей цепи
Приложения:

Ответы
Автор ответа:
0
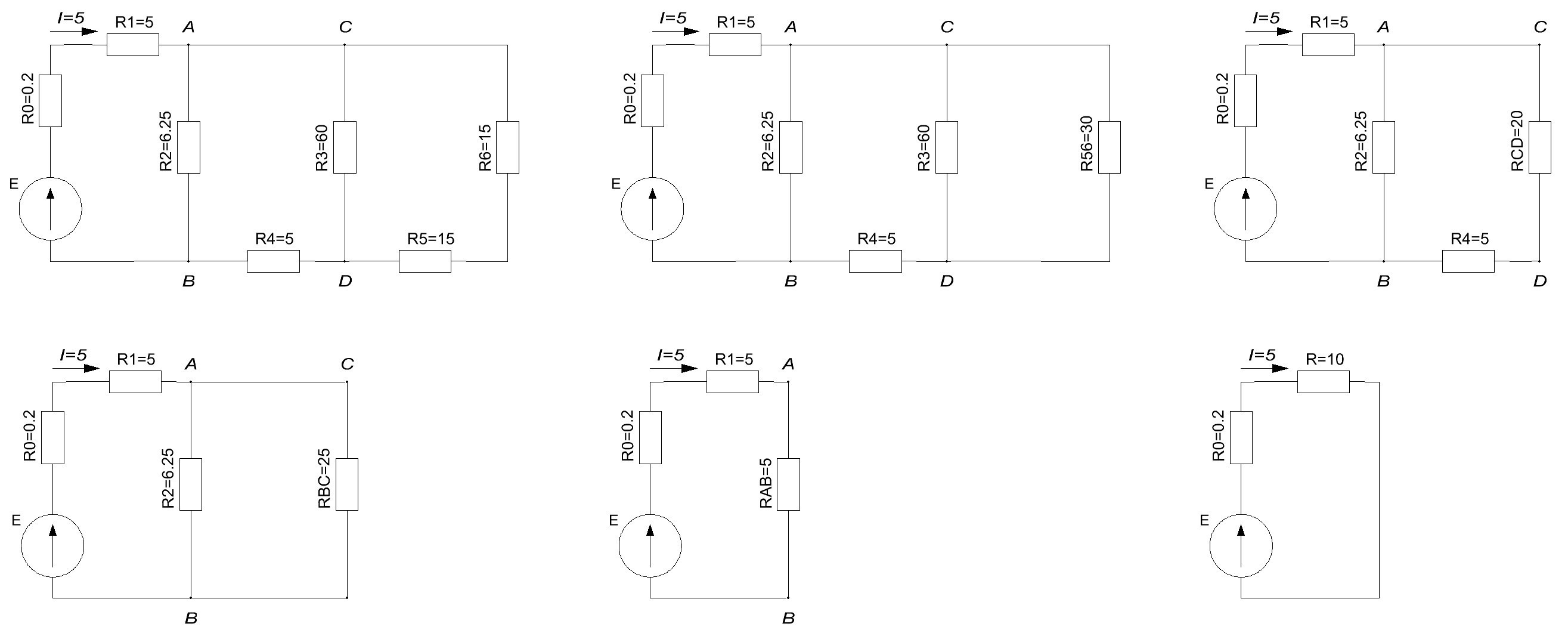
В цепи один источник ЭДС и несколько контуров. Определим эквивалентное сопротивление внешней цепи, для чего будем последовательно упрощать схему (см. вложение 1).
1. Резисторы R₅ и R₆ включены последовательно. Их эквивалентное сопротивление R₅₆=R₅+R₆=15+15=30 (Ом). Заменим эти два резистора эквивалентом R₅₆.
2. Резисторы R₃ и R₅₆ включены параллельно. Их эквивалентное сопротивление

Заменим эти два резистора эквивалентом RCD
3. Резисторы R₄ и RCD включены последовательно. Их эквивалентное сопротивление RBC=R₄+RCD=5+20=25 (Ом). Заменим эти два резистора эквивалентом RBC.
4. Резисторы R₂ и RBC включены параллельно. Их эквивалентное сопротивление

Заменим эти два резистора эквивалентом RAB.
5. Резисторы R₁ и RAB включены последовательно. Их эквивалентное сопротивление R=R₁+RAB=5+5=10 (Ом). Заменим эти два резистора эквивалентом R.
6. По закону Ома для полной цепи

Далее будем использовать закон Ома для участка цепи и следствие из него::

Кроме того, будем пользоваться формулой для расчета мощности, выделяемой на сопротивлении

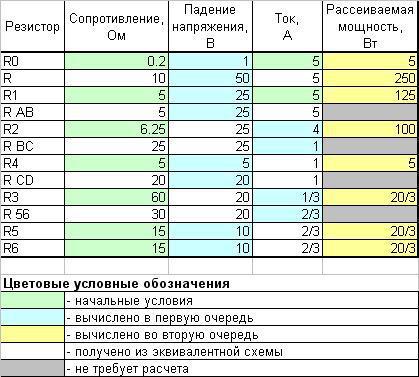
Результаты расчета приведены в таблице (вложение 2).
Полная мощность, рассеиваемая в цепи: P=E×I=51×5=225 (Вт).
Проверим расчет с помощью баланса мощностей. Полная рассеиваемая мощность должна быть равна сумме мощностей, рассеиваемых на каждом элементе цепи.

Равенство выполняется, следовательно, расчет выполнен верно.
1. Резисторы R₅ и R₆ включены последовательно. Их эквивалентное сопротивление R₅₆=R₅+R₆=15+15=30 (Ом). Заменим эти два резистора эквивалентом R₅₆.
2. Резисторы R₃ и R₅₆ включены параллельно. Их эквивалентное сопротивление
Заменим эти два резистора эквивалентом RCD
3. Резисторы R₄ и RCD включены последовательно. Их эквивалентное сопротивление RBC=R₄+RCD=5+20=25 (Ом). Заменим эти два резистора эквивалентом RBC.
4. Резисторы R₂ и RBC включены параллельно. Их эквивалентное сопротивление
Заменим эти два резистора эквивалентом RAB.
5. Резисторы R₁ и RAB включены последовательно. Их эквивалентное сопротивление R=R₁+RAB=5+5=10 (Ом). Заменим эти два резистора эквивалентом R.
6. По закону Ома для полной цепи
Далее будем использовать закон Ома для участка цепи и следствие из него::
Кроме того, будем пользоваться формулой для расчета мощности, выделяемой на сопротивлении
Результаты расчета приведены в таблице (вложение 2).
Полная мощность, рассеиваемая в цепи: P=E×I=51×5=225 (Вт).
Проверим расчет с помощью баланса мощностей. Полная рассеиваемая мощность должна быть равна сумме мощностей, рассеиваемых на каждом элементе цепи.
Равенство выполняется, следовательно, расчет выполнен верно.
Приложения:
Автор ответа:
0
ЭДС найдена в п.6
Автор ответа:
0
огромное Вам спасибо
Автор ответа:
0
*понимание
Автор ответа:
0
Ну, Ваше непонимание - это же Ваша проблема, чего прощения просить?)
Похожие вопросы
Предмет: Математика,
автор: isysxristos
Предмет: Українська мова,
автор: theminecraftxboxone
Предмет: История,
автор: miroslavbarusiavicus
Предмет: Математика,
автор: сано25679
Предмет: Математика,
автор: daryarudnevskay