Question

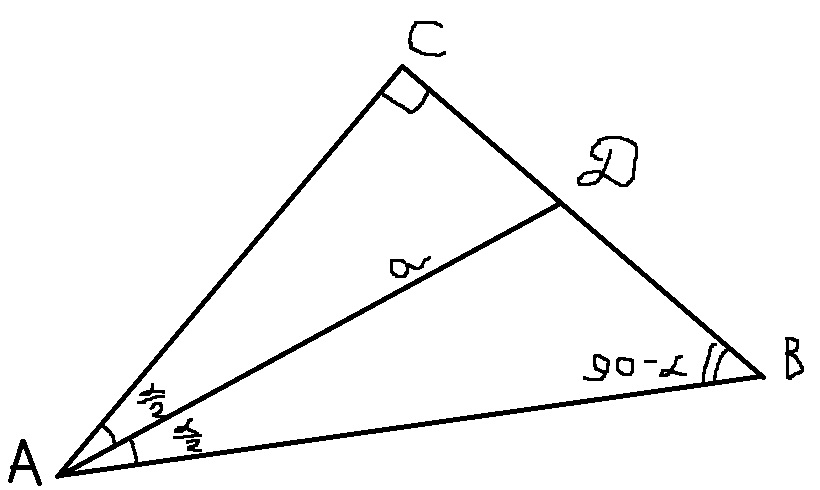
В треугольнике ABC угол C 90 градусов, биссектриса AD равна a, угол A = альфа. Найдите BD. Если можно, подробным решением) буду благодарна!) заранее спасибо:3

Answer 1

Для начала рассмотрим треугольник ACD. Вычислим катет АС. Здесь АD - гипотенуза, угол CAD равен $angle CAD=frac{alpha}{2}$ по определению биссектрисы AD.

 

$AC=a*cos</var><var>angle CAD$

 

$AC=a*cos</var><var><var>frac{alpha}{2}</var>$

 

Катет CD равен

$CD=a*sin</var><var></var><var>angle CAD$

 

$CD=a*sinfrac{alpha}{2}$

 

Теперь рассмотри исходный треугольник АВС. Найдем в нем другой катет СВ. Так как

 

$angle CAB=alpha,$

 

то $CB=AC*tanangle CAB$

 

$CB=AC*tan</var><var>alpha$

 

$CB=<var>a*cos</var><var><var>frac{alpha}{2}</var></var>*tan</var><var>alpha$

 

Заметим, что BD=CB-CD

 

$BD=a*cosfrac{alpha}{2}*tanalpha-<var>a*sinfrac{alpha}{2}</var>$

 

$BD=a*left(cosfrac{alpha}{2}*tanalpha-sinfrac{alpha}{2}right)$

 

Можно, конечно, упростить, но  как-то неохота, да и будет ли проще?