Предмет: Физика,
автор: Maximonchik
Сосновая доска длиной 6 м лежит на опоре, выступая за нее одним концом на 1 м, а вторым концом погрузившись в воду. Найдите длину погруженной в воду части бревна.
Ответы
Автор ответа:
0
ρ₁ = 1000 кг/м³ -- плотность воды
ρ₂ = 520 кг/м³ -- плотность сосны
S -- площадь поперечного сечения доски
Условие равновесия рычага: Fa·(5 - х/2) + Fт₁·1/2 = Fт₅·5/2.
ρ₁·g·S·x·(5 - х/2) + ρ₂·S·1·g·1/2 = ρ₂·S·5·g·5/2
ρ₁·g·S·x·(5 - х/2) = 12·ρ₂·S·g
ρ₁·x·(5 - х/2) = 12·ρ₂
ρ₁·x·(10 - х) = 24·ρ₂
1000·x·(10 - х) = 24·520
25·x·(10 - х) = 24·13
250х - 25х² = 312
25х² - 250х + 312 = 0
D = 62500 - 31200 = 31300

Погружённый в воду конец доски не может быть больше 5 м, поэтому:
 ≈ 1,46 м
≈ 1,46 м
ρ₂ = 520 кг/м³ -- плотность сосны
S -- площадь поперечного сечения доски
Условие равновесия рычага: Fa·(5 - х/2) + Fт₁·1/2 = Fт₅·5/2.
ρ₁·g·S·x·(5 - х/2) + ρ₂·S·1·g·1/2 = ρ₂·S·5·g·5/2
ρ₁·g·S·x·(5 - х/2) = 12·ρ₂·S·g
ρ₁·x·(5 - х/2) = 12·ρ₂
ρ₁·x·(10 - х) = 24·ρ₂
1000·x·(10 - х) = 24·520
25·x·(10 - х) = 24·13
250х - 25х² = 312
25х² - 250х + 312 = 0
D = 62500 - 31200 = 31300
Погружённый в воду конец доски не может быть больше 5 м, поэтому:
Приложения:

Автор ответа:
0
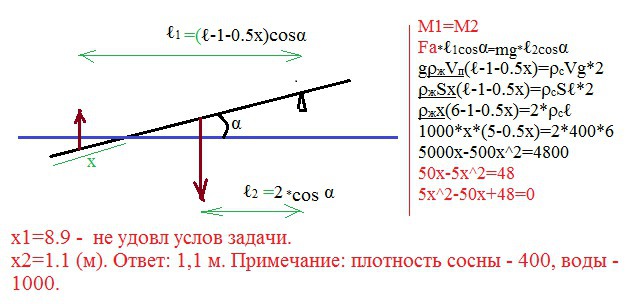
Решение задачи на фото.
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: anastasiakolodka6
Предмет: Математика,
автор: hodarinovaemilia
Предмет: Химия,
автор: kalinina94
Предмет: Алгебра,
автор: RyzhovaNastyusa
Предмет: Биология,
автор: mariyavgg