Предмет: Математика,
автор: Stydent29ru
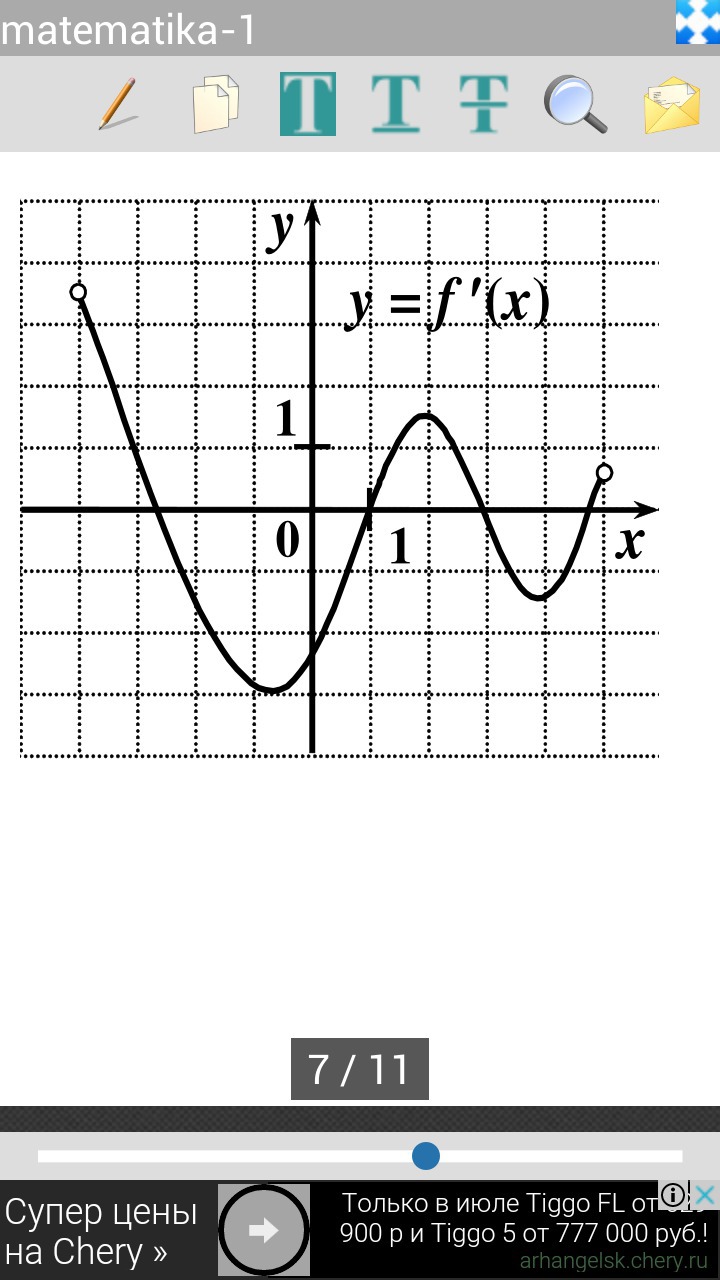
На рисунке изображен график её производной.
Найдите число касательных к графику функции
y = f (x), которые наклонены к положительному
направлению оси абсцисс под углом 45°.
y = f (x)
Приложения:
Ответы
Автор ответа:
0
Число касательных, образующих угол в 45° к положительному направлению оси ОХ, равно 3, так как количество точек пересечения графика производной y=f '(x) с прямой у=1 всего три.
f '(x0)=tgα , где α - угол наклона касательной к положительному направлению оси ОХ, tg45°=1 ⇒ надо подсчитать количество точек пересечения графика у=f '(x) и у=1 ( у=1 - прямая, параллельная оси ОХ, отстоящая от неё на расстояние, равное 1 ) .
f '(x0)=tgα , где α - угол наклона касательной к положительному направлению оси ОХ, tg45°=1 ⇒ надо подсчитать количество точек пересечения графика у=f '(x) и у=1 ( у=1 - прямая, параллельная оси ОХ, отстоящая от неё на расстояние, равное 1 ) .
Автор ответа:
0
Так ведь касательная проводится к графику функции, а на рисунке дан график производной. К этому графику никаких касательных не проводится.
Похожие вопросы
Предмет: Математика,
автор: Leonelle
Предмет: Другие предметы,
автор: bunny89
Предмет: Математика,
автор: nastyasavhenko15
Предмет: Математика,
автор: 09423iwe8r
Предмет: Математика,
автор: FominArtyom200