Предмет: Математика,
автор: radoduna
Найти все x удовлетворяющие неравенству. (вложено)
Совершенно не знаю как делать этот номер, мне бы образец решения)
Приложения:
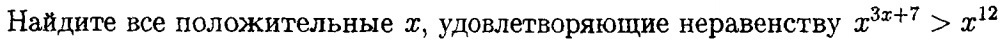
Ответы
Автор ответа:
0
x^(3x+7)>x^12
1) Пусть x>1
Тогда
3x+7>12
3x>5
x>5/3 сравнивая с ОДЗ(x>1) получаем x>5/3
2) Пусть 0<x<1
Тогда
3x+7<12
3x<5
x<5/3 Сравнивая с ОДЗ(0<x<1), получаем 0<x<1
3) Пусть x<0
Тогда x^12 число положительное
Значит x^(3x+7)- тоже число положительное
При этом 3х+7>12
3x>5
x>5/3 сравниваем с ОДЗ( x<0) , получаем x пустое множество
1) Пусть x>1
Тогда
3x+7>12
3x>5
x>5/3 сравнивая с ОДЗ(x>1) получаем x>5/3
2) Пусть 0<x<1
Тогда
3x+7<12
3x<5
x<5/3 Сравнивая с ОДЗ(0<x<1), получаем 0<x<1
3) Пусть x<0
Тогда x^12 число положительное
Значит x^(3x+7)- тоже число положительное
При этом 3х+7>12
3x>5
x>5/3 сравниваем с ОДЗ( x<0) , получаем x пустое множество
Автор ответа:
0
Правильный ответ следующий X принадлежит (0;1) U (5/3; +бесконечность)
Автор ответа:
0
Пункт номер 2. Там же все написано
Автор ответа:
0
Т.е. методом подстановки значения мы определяем знак, а после на оси координат отмечаем промежутки, верно?
Автор ответа:
0
Так как правая часть всегда положительная независимо от параметра Х, то
3х+7>12
Х>5/3
Похожие вопросы
Предмет: Русский язык,
автор: nika1872
Предмет: Английский язык,
автор: dizanyflor
Предмет: Физика,
автор: gerasimsgsp
Предмет: Математика,
автор: All0
Предмет: Алгебра,
автор: TudiMenka