Предмет: Математика,
автор: sashahan
Помогите решить
Очень нужна помощь, у меня получается следующее выражение
Я решаю примерно так, но это система уравнений, и тут должны быть значения от бла бла до бла бла, как их решать помогите пожалуйста, в интернете слишком много лишнего пишут я не пойму, лучше посмотреть как их решать, чем читать и не понимать

Приложения:
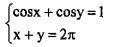
Ответы
Автор ответа:
0
x=2π-y
cos(2π-y)+cosy=1
cosy+cosy=1
2cosy=1
cosy=1/2
y=-π/3⇒x=2π+π/3=8π/3
y=π/3⇒x=2π-π/3=5π/3
cos(2π-y)+cosy=1
cosy+cosy=1
2cosy=1
cosy=1/2
y=-π/3⇒x=2π+π/3=8π/3
y=π/3⇒x=2π-π/3=5π/3
Автор ответа:
0
Оно не подходит
Автор ответа:
0
Ответы примерно в таком виде, (pi/3+2pin;-pi/3+2(1-n)) по типу того, я не знаю правильный это ответ или нет, однако ответ должен быть типо того, как прийти к такому ответу?
Автор ответа:
0
Из второо уравнения находим y=2*π-x. Подставляя это значение в первое уравнение и учитывая, что cos(y)=cos(2*π-x)=cos(x), получаем уравнение 2*cos(x)=1, откуда cos(x)=1/2, x1=π/3+2*π*n, x2=-π/3+2*π*n, n∈Z. Тогда y1=2*π-x1=5*π/3-2*π*n, y2=2*π-x2=7*π/3-2*π*n.
Ответ: (π/3+2*π*n; 5*π/3-2*π*n), (-π/3+2*π*n; 7*π/3-2*π*n), n∈Z.
Ответ: (π/3+2*π*n; 5*π/3-2*π*n), (-π/3+2*π*n; 7*π/3-2*π*n), n∈Z.
Похожие вопросы
Предмет: Русский язык,
автор: dominibogzlata10
Предмет: Математика,
автор: alinapilipisin9
Предмет: История,
автор: melyasomova00
Предмет: Алгебра,
автор: АnyaKilina