Предмет: Математика,
автор: VeronikaKokorina1
найдите сумму первых н членов геометрической прогрессии если в7 = 16/9 ; q =2/3 ; n=7
Ответы
Автор ответа:
0
b7 = b1*q^6 => b1 = b7/q^6
b1 = 16/9 / (2/3)^6=16/9 * (3/2)^6=(2^4*3^6)/(3^2*2^6)=3^4/2^2=81/4
Sn=b1*(q^n-1)/(q-1)
S7=81/4 * ((2/3)^7-1) / (2/3 - 1) = 81/4 * (2^7/3^7 - 1) / (-1/3) = 3^4/2^2 * (2^7/3^7-1) * (-3) = -3^5/2^2 * 2^7/3^7 + 3^5/2^2 = 3^5/2^2 - (3^5*2^7)/(2^2*3^7)=243/4-32/9=(243*9-32*4)/(9*4)=2059/36.
b1 = 16/9 / (2/3)^6=16/9 * (3/2)^6=(2^4*3^6)/(3^2*2^6)=3^4/2^2=81/4
Sn=b1*(q^n-1)/(q-1)
S7=81/4 * ((2/3)^7-1) / (2/3 - 1) = 81/4 * (2^7/3^7 - 1) / (-1/3) = 3^4/2^2 * (2^7/3^7-1) * (-3) = -3^5/2^2 * 2^7/3^7 + 3^5/2^2 = 3^5/2^2 - (3^5*2^7)/(2^2*3^7)=243/4-32/9=(243*9-32*4)/(9*4)=2059/36.
Автор ответа:
0
решение!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Приложения:
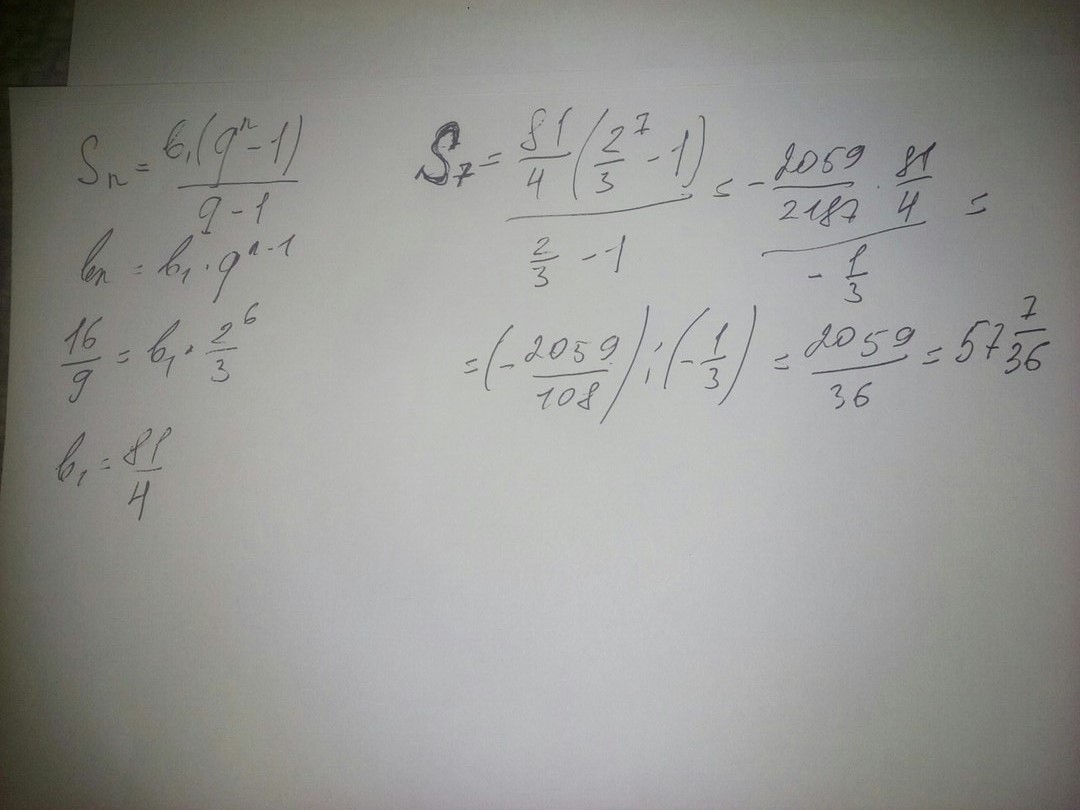
Похожие вопросы
Предмет: Биология,
автор: aysasalamova
Предмет: Обществознание,
автор: Adalv8002
Предмет: Английский язык,
автор: katicheva23
Предмет: Математика,
автор: 380679671354
Предмет: Литература,
автор: ilikrestochka