Предмет: Геометрия,
автор: Аноним
около Круга радиуса к описан ромб с углом 150 градусов Найдите площадь ромба
Ответы
Автор ответа:
0
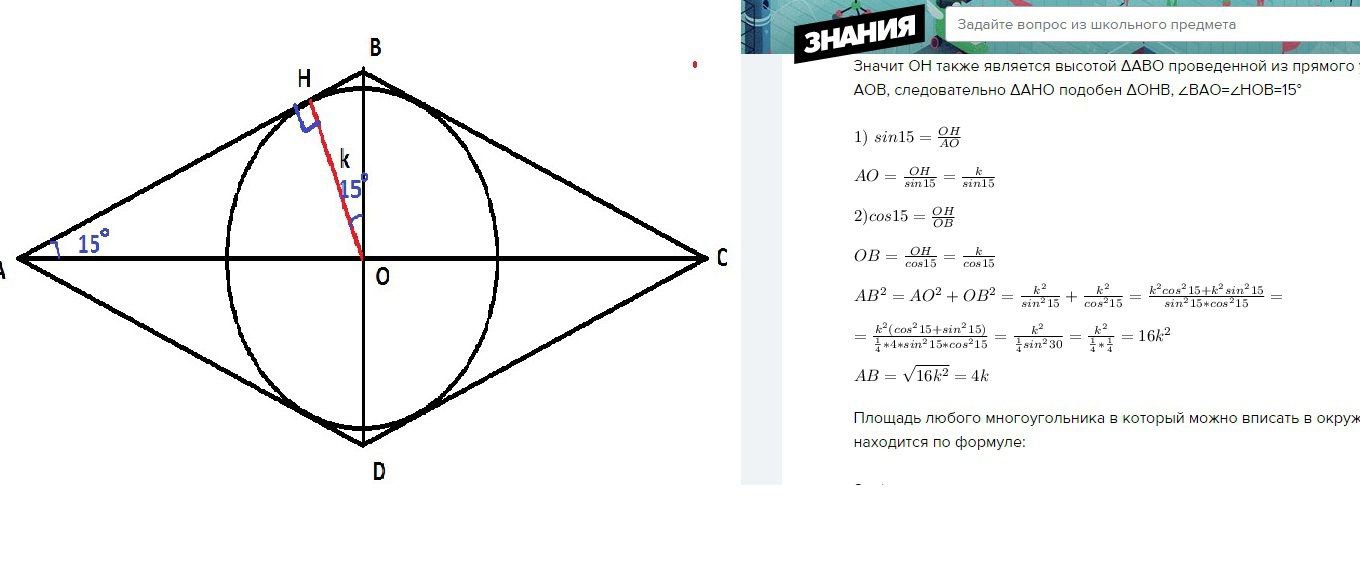
Дано: ABCD-ромб, ∠В-150°, k-радиус вписанного круга.
Если ∠В=150°, то ∠А=180°-∠В=180°-150°=30°
диагонали АС и BD-пересекаются под прямым углом и делят ромб пополам, то есть АС и BD-биссектрисы, значит О-центр круга и ∠ВАО=30°/2=15°
проведем радиус в точку касания Н. (радиус проведенный в точку касания перпендикулярен самой касательной)
Значит ОН также является высотой ΔАВО проведенной из прямого угла АОВ, следовательно ΔАНО подобен ΔОНВ, ∠BAO=∠HOB=15°
(ЕСЛИ ТЕКСТ НИЖЕ ПОЛНОСТЬЮ НЕ ОТОБРАЖАЕТСЯ, ТО ПОСМОТРИ СКРИН)

Площадь любого многоугольника в который можно вписать в окружность находится по формуле:
S=p*r, где p-полупериметр
p=4*AB/2=4*4k/2=8k
S=8k*k=8k²
Ответ: 8k²
Если ∠В=150°, то ∠А=180°-∠В=180°-150°=30°
диагонали АС и BD-пересекаются под прямым углом и делят ромб пополам, то есть АС и BD-биссектрисы, значит О-центр круга и ∠ВАО=30°/2=15°
проведем радиус в точку касания Н. (радиус проведенный в точку касания перпендикулярен самой касательной)
Значит ОН также является высотой ΔАВО проведенной из прямого угла АОВ, следовательно ΔАНО подобен ΔОНВ, ∠BAO=∠HOB=15°
(ЕСЛИ ТЕКСТ НИЖЕ ПОЛНОСТЬЮ НЕ ОТОБРАЖАЕТСЯ, ТО ПОСМОТРИ СКРИН)
Площадь любого многоугольника в который можно вписать в окружность находится по формуле:
S=p*r, где p-полупериметр
p=4*AB/2=4*4k/2=8k
S=8k*k=8k²
Ответ: 8k²
Приложения:
Похожие вопросы
Предмет: Математика,
автор: aylaismaylova
Предмет: Геометрия,
автор: ilyas270778
Предмет: Физика,
автор: Lonson33377
Предмет: Химия,
автор: elena1953
Предмет: Математика,
автор: Alina352