Предмет: Математика,
автор: rybkakatrin
Исследовать сходимость положительного ряда, применяя какой – либо из достаточных признаков сходимости (сравнения, Даламбера, радикальный или интегральный)
Приложения:
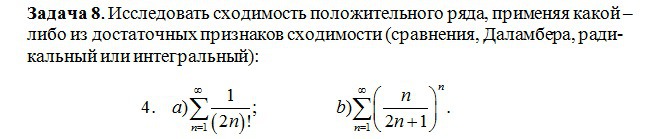
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: История,
автор: sonyaaa1232873
Предмет: Українська мова,
автор: 4SVSHNIK21
Предмет: Українська мова,
автор: yaroslavyefymovych
Предмет: Алгебра,
автор: diankalazovska
Предмет: Математика,
автор: elenashestakova