Предмет: Математика,
автор: alekcevizalov11
ребята решите пожалуйста и очень важно назовите тему по математике к которой уравнение относится , что бы потом найти этому подобные выражения .Самому надо порешать .
Приложения:
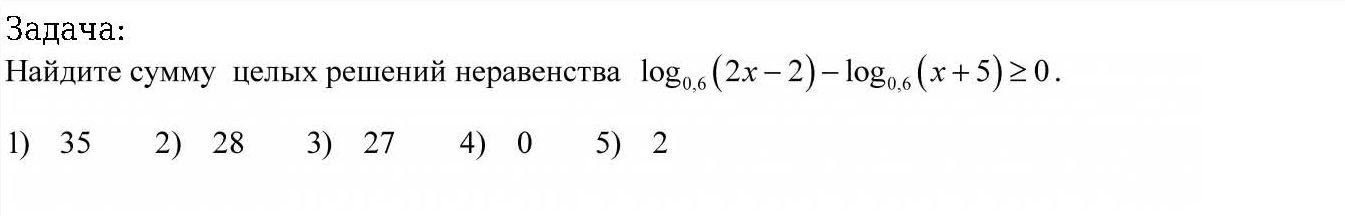
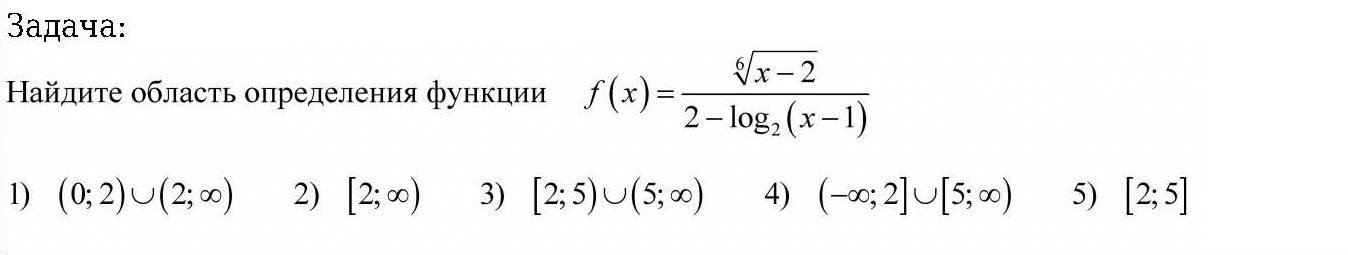
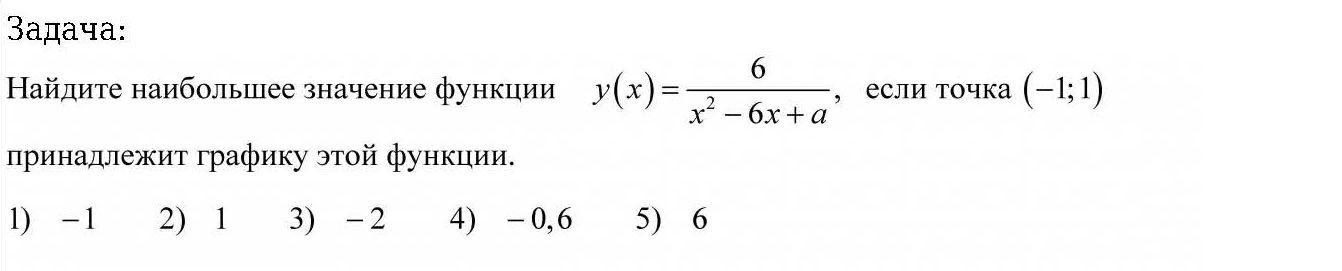
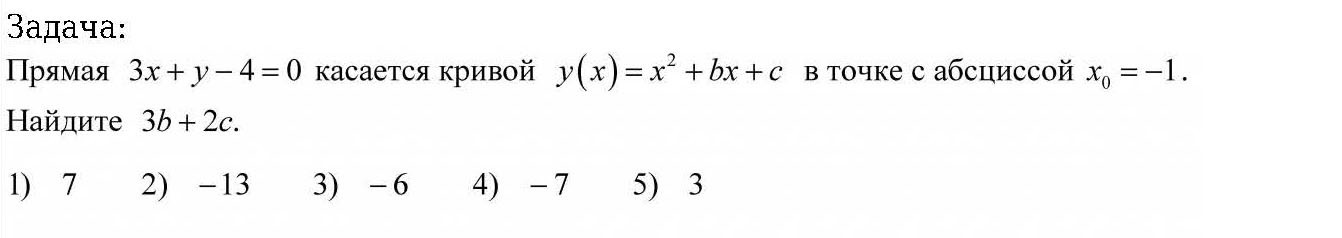

Ответы
Автор ответа:
0
1) Логарифмические неравенства.
![log_{0,6}(2x-2)-log_{0,6}(x+5)geq0, \ log_{0,6}(2x-2)geqlog_{0,6}(x+5), \ 0,6 textless 1, \ left { {{2x-2leq x+5,} atop {2x-2 textgreater 0,}} right. left { {{xleq7,} atop {x textgreater 1,}} right. 1 textless xleq 7, \ xin(1;7]; \ 2+3+4+5+6+7=27. log_{0,6}(2x-2)-log_{0,6}(x+5)geq0, \ log_{0,6}(2x-2)geqlog_{0,6}(x+5), \ 0,6 textless 1, \ left { {{2x-2leq x+5,} atop {2x-2 textgreater 0,}} right. left { {{xleq7,} atop {x textgreater 1,}} right. 1 textless xleq 7, \ xin(1;7]; \ 2+3+4+5+6+7=27.](https://tex.z-dn.net/?f=log_%7B0%2C6%7D%282x-2%29-log_%7B0%2C6%7D%28x%2B5%29geq0%2C+%5C+log_%7B0%2C6%7D%282x-2%29geqlog_%7B0%2C6%7D%28x%2B5%29%2C+%5C+0%2C6+textless++1%2C+%5C++left+%7B+%7B%7B2x-2leq+x%2B5%2C%7D+atop+%7B2x-2+textgreater++0%2C%7D%7D+right.+left+%7B+%7B%7Bxleq7%2C%7D+atop+%7Bx+textgreater++1%2C%7D%7D+right.++1+textless++xleq+7%2C+%5C+xin%281%3B7%5D%3B+%5C+2%2B3%2B4%2B5%2B6%2B7%3D27.)
2) Область определения функции.
![f(x)=frac{sqrt[6]{x-2}}{2-log_2(x-1)}, \ left{begin{array}{c} x-2 geq 0, \ 2-log_2(x-1)neq0, \ x-1 textgreater 0; end{array}right. left{begin{array}{c} xgeq2, \ log_2(x-1)neq2, \ x textgreater 1; end{array}right. left { {{x geq 2,} atop {x-1 neq 4,}} right. left { {{x geq 2,} atop {x neq 5,}} right. \ xin[2;5)cup(5;+infty). f(x)=frac{sqrt[6]{x-2}}{2-log_2(x-1)}, \ left{begin{array}{c} x-2 geq 0, \ 2-log_2(x-1)neq0, \ x-1 textgreater 0; end{array}right. left{begin{array}{c} xgeq2, \ log_2(x-1)neq2, \ x textgreater 1; end{array}right. left { {{x geq 2,} atop {x-1 neq 4,}} right. left { {{x geq 2,} atop {x neq 5,}} right. \ xin[2;5)cup(5;+infty).](https://tex.z-dn.net/?f=f%28x%29%3Dfrac%7Bsqrt%5B6%5D%7Bx-2%7D%7D%7B2-log_2%28x-1%29%7D%2C+%5C+left%7Bbegin%7Barray%7D%7Bc%7D+x-2+geq+0%2C+%5C+2-log_2%28x-1%29neq0%2C+%5C+x-1+textgreater++0%3B+end%7Barray%7Dright.+left%7Bbegin%7Barray%7D%7Bc%7D+xgeq2%2C+%5C+log_2%28x-1%29neq2%2C+%5C+x+textgreater++1%3B+end%7Barray%7Dright.++left+%7B+%7B%7Bx+geq+2%2C%7D+atop+%7Bx-1+neq+4%2C%7D%7D+right.+left+%7B+%7B%7Bx+geq+2%2C%7D+atop+%7Bx+neq+5%2C%7D%7D+right.+%5C+xin%5B2%3B5%29cup%285%3B%2Binfty%29.)
3) Наибольшее и наименьшее значение функции (экстремумы функции)

4) Уравнение касательной к графику функции.

5) Физический смысл производной.

2) Область определения функции.
3) Наибольшее и наименьшее значение функции (экстремумы функции)
4) Уравнение касательной к графику функции.
5) Физический смысл производной.
Похожие вопросы
Предмет: Алгебра,
автор: Alexsandr004
Предмет: Русский язык,
автор: xaxaxxxaxaxaxaxaxxxa
Предмет: Математика,
автор: solerass
Предмет: Математика,
автор: aleksandra23017