Предмет: Математика,
автор: rybkakatrin
Задача 1. Даны матрицы А и В и . Е - единичная матрица. Найти:
а) матрицу (А-2Е)*В ; б) обратную матрицу А^-1 и проверить, что А^-1*А=Е
Приложения:
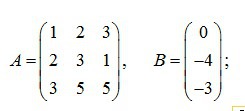
Ответы
Автор ответа:
0
Решение смотрите в приложении...
Приложения:

Автор ответа:
0
Приложения:

Похожие вопросы
Предмет: Математика,
автор: solerass
Предмет: Другие предметы,
автор: Assasin22076
Предмет: Математика,
автор: Аноним
Предмет: Физика,
автор: yuliyagalkina