Предмет: Математика,
автор: aatm
Помогите найти наименьшее целое целое решение неравенства
Приложения:
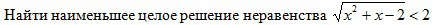
Ответы
Автор ответа:
0
√(x²+x-2)<2
ОДЗ: x²+x-2=(x-1)(x+2)>=0 => x∈(-∞;-2]∪[1;+∞)
Возведем в квадрат обе части неравенства.
x²+x-2<4
x²+x-6<0
(x-2)(x+3)<0
x∈(-3;2)
С учетом ОДЗ получим: x∈(-3;-2]∪[1;2)
ОДЗ: x²+x-2=(x-1)(x+2)>=0 => x∈(-∞;-2]∪[1;+∞)
Возведем в квадрат обе части неравенства.
x²+x-2<4
x²+x-6<0
(x-2)(x+3)<0
x∈(-3;2)
С учетом ОДЗ получим: x∈(-3;-2]∪[1;2)
Автор ответа:
0
Спасибо)
Автор ответа:
0
От одного до двух ответ
Похожие вопросы
Предмет: Математика,
автор: dora6410
Предмет: Английский язык,
автор: brawldima4555
Предмет: Алгебра,
автор: klyukinruslan
Предмет: Математика,
автор: yulyapavlova91
Предмет: Обществознание,
автор: bushlanovadina