Предмет: Математика,
автор: QuasarDreemov
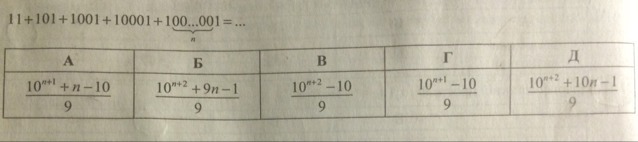
Найдите правило, по которому можно записать прогрессию.
Приложения:
Ответы
Автор ответа:
0
видимо по первое вопрос
1+10ⁿ
1+10ⁿ
Автор ответа:
0
...?) Какому выражению может быть тождественна данная сумма? (Ответ Б, но как к этому прийти).
Автор ответа:
0
Запишем cумму так:

Здесь n=0, 1, 2, 3...
Теперь применим к десяткам формулу суммы n+1 членов геометрической прогрессии с первым членом 10 и знаменателем 10. И прибавим к этой сумме n+1 единиц.

Здесь n=0, 1, 2, 3...
Теперь применим к десяткам формулу суммы n+1 членов геометрической прогрессии с первым членом 10 и знаменателем 10. И прибавим к этой сумме n+1 единиц.
Автор ответа:
0
В сумме у тебя было какое-то количество единиц. Потом ты записал сумму геом прогрессии + n + 1. Почему только одна единица?
Автор ответа:
0
Потому что единиц в этой сумме n+1. Отсчет то мы начинаем с нуля.
Автор ответа:
0
Извините, я не понял. У нас были числа, у которых в разряде единиц были единицы. Мы их записали отдельно и ещё + n. Но почему тогда это n+1? И какой отсчёт от нуля?
Автор ответа:
0
Не знаю как объяснить. Если n=0, единица в сумме одна, если n=1 единицы две. Вот и получается что их n+1
Автор ответа:
0
Почему при n=0, сумма единиц равна 1? У нас же было как минимум пять чисел в разряде с единицей, значит там как минимум пять единиц и ещё плюс n?
Похожие вопросы
Предмет: Немецкий язык,
автор: Filinos
Предмет: География,
автор: namjoon61
Предмет: Математика,
автор: dmitrygorbachev29
Предмет: Математика,
автор: alena20036
Предмет: Алгебра,
автор: MashaSnejp