Предмет: Алгебра,
автор: АлинаКагарманова
упррастите выражение (фото)
Приложения:
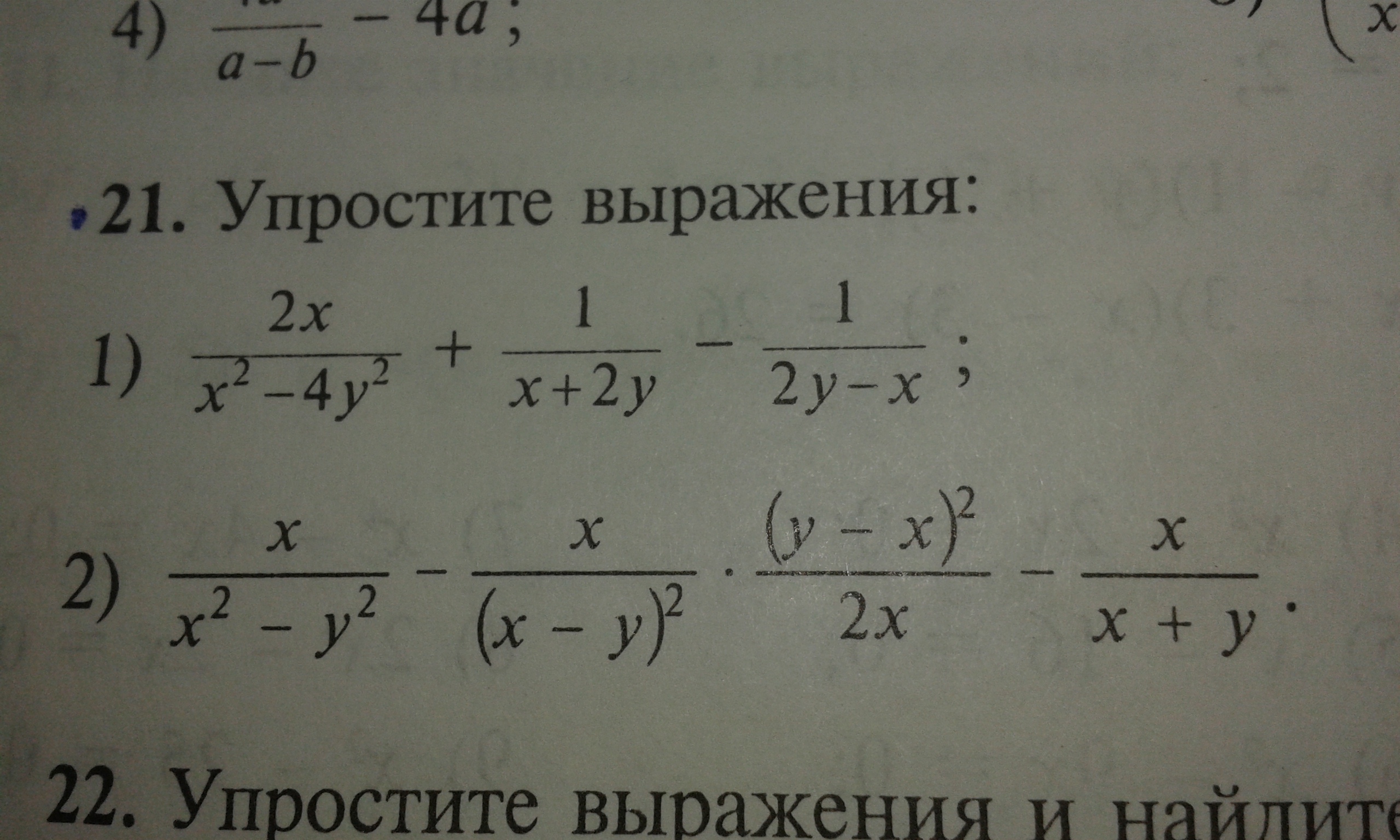
Ответы
Автор ответа:
0
1.

2.


2.
Похожие вопросы
Предмет: Другие предметы,
автор: Аноним
Предмет: Биология,
автор: stasbomz7
Предмет: Математика,
автор: vixiplay54
Предмет: Химия,
автор: dimakhamidov9
Предмет: Математика,
автор: OneDam