Question

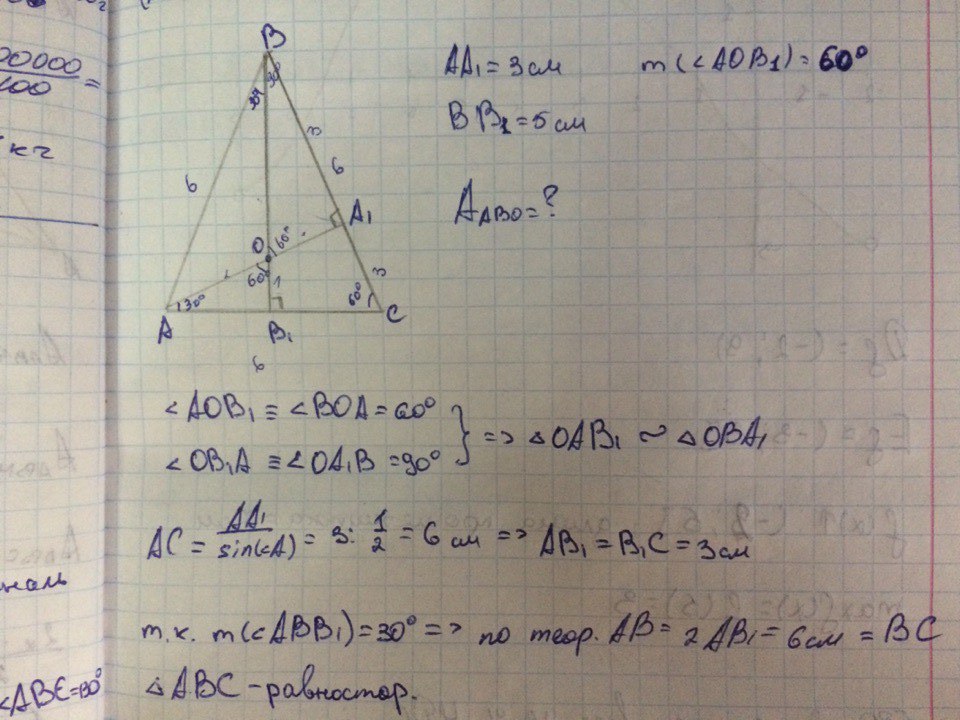
В остроугольном треугольнике ABC высоты AA1 и BB1 пересекаются в точке О и величина угла AOB=6. Найти площадь треугольника ABO, если АА1= 3 см и ВВ1 = 5 см.
( я тут не много набросал, помогите кто знает как решить)

Answer 1

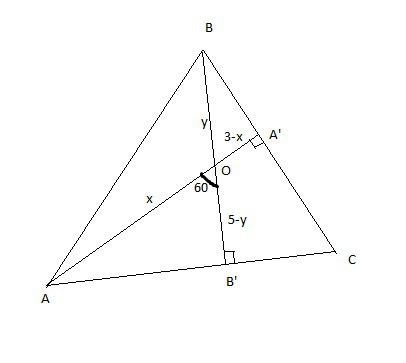
Обозначим AO=x, OA1=3-x, BO=y, OB1=5-y.
Тогда из треугольника AOB1: OB1=AO*cos∠AOB1,
Из треугольника A1OB: A1O=BO*cos∠BOA1
Получим систему уравнений
5-y=x*cos(60°)
3-x=y*cos(60°)
_____
2(5-y)=x
2(3-x)=y
______
10-2y=x
6-2x=y
_____
Подставим первое уравнение во второе. Получим:
6-2(10-2y)=y
6-20+4y=y
y=14/3
x=10-2*(14/3)=2/3
Тогда S_AOB=1/2*AO*OB*sin∠AOB=1/2*x*y*sin(120°)=1/2*2/3*14/3*√3/2=7√3/9