Question

В прямоугольном треугольнике найдите отношение меньшего катета к большему, если высота и медиана, выходящие из вершины прямого угла относятся, как 9:15.
Объясните как решить.

Answer 1

Прошу прощение за качество, поясню если что-то непонятно. 

Answer 2

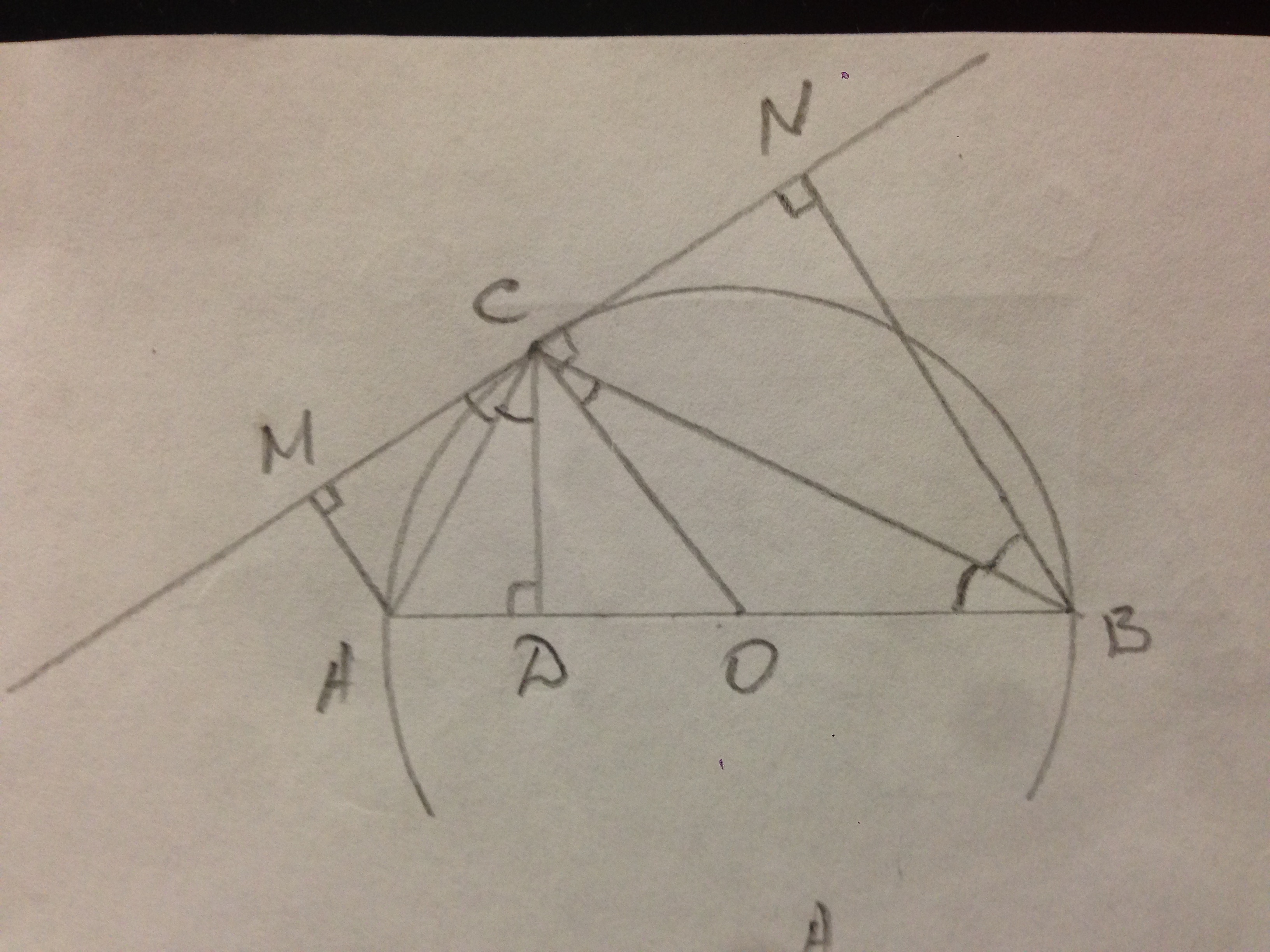
(Рисунок от другой задачи, нужно откинуть лишнее).

В треугольнике АВС СО - медиана, СД - высота, СД:СО=9:15.
Пусть одна часть в заданном отношении равна х, тогда СД=9х, СО=15х.
В прямоугольном тр-ке медиана гипотенузы равна её половине, значит АВ=2СО=30х, АО=СО=15х.
В тр-ке АСД ОД=√(СО²-СД²)=√х²·(15²-9²)=12х.
АД=АО-ДО=15х-12х=3х.
В тр-ке АСД АС=√(АД²+СД²)=√х²·(3²+9²)=х√90=3х√10.
В тр-ке АВС ВС=√(АВ²-АС²)=√х²·(30²-90)=х√810=9х√10.
Итак, АС:ВС=(3х√10):(9х√10)=1:3 - это ответ.

Answer 3

Можно было эти корни из 10 не считать. Из подобия треугольников ACD и ABC, искомое отошение равно AD/CD=1/3.

Answer 4

Можно.