Предмет: Физика,
автор: UmbertoVargas
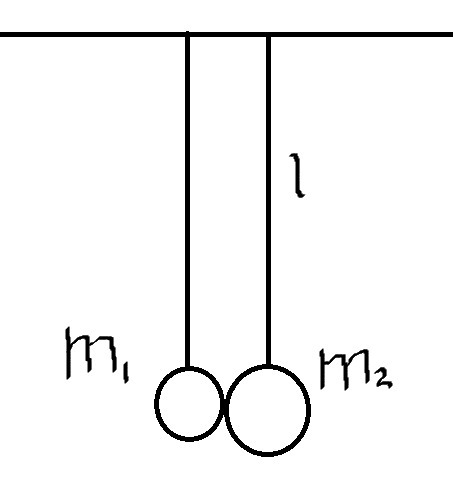
Два абсолютно упругих шарика с массами m1 = 100 г и m2 = 300 г подвешены на одинаковых нитях длины l = 50 см каждая (см. рис.). Первый шарик отклоняют от положения равновесия на угол α = 90° и отпускают. На какую высоту поднимется второй шарик после соударения?
Приложения:
Ответы
Автор ответа:
0
Закон созранения энергии:
m1gL=m1vo^2/2
vo=√2gL=3.16 м/с;
Система уравнений из закона созранения импульса и энергии:
1)m1vo=m2v2-m1v1;
2)m1vo^2/2=m2v2^2/2+m1v1^2/2;
1)3.16=3v2-v1;
2)10=3v2^2+v1^2;
1)v1=3v2-3.16;
2)10=3v2^2+9v2^2-19v2+10
12v2=19
v2=1.6 м/с
Закон сохранения энергии:
gh=v2^2/2;
h=v2^2/2g=12.8 см(если хотите ближе к ответу-возьмите g за 9.81 и пересчитайте)
Автор ответа:
0
при 9.81 ответ наоборот увеличится и получится 13.06 см
Автор ответа:
0
v2=1,58113883 м/с
h=0,125 м
h=0,125 м
Автор ответа:
0
vo=3,16227766
Автор ответа:
0
при g=10
Автор ответа:
0
кстати, величина g на ответ не влияет
Автор ответа:
0
1) опускание шарика 1
m1*g*L =m1*v^2/2
v=корень(2*g*L)
2) столковение двух шаров
m1*v=m1*u1+m2*u2
m1*v^2/2=m1*u1^2/2+m2*u2^2/2
отсюда u2=2*m1*v/(m1+m2)=2*m1*корень(2*g*L)/(m1+m2)
3) подъем шарика 2
m2*u2^2/2=m2*g*H
H=u2^2/(2*g) =(2*m1*корень(2*g*L)/(m1+m2))^2/(2*g) =
=L*(2*m1/(m1+m2))^2 = 4*L/(1+m2/m1)^2 = 4*0,5/(1+0,3/0,1)^2 = 0,125 м
m1*g*L =m1*v^2/2
v=корень(2*g*L)
2) столковение двух шаров
m1*v=m1*u1+m2*u2
m1*v^2/2=m1*u1^2/2+m2*u2^2/2
отсюда u2=2*m1*v/(m1+m2)=2*m1*корень(2*g*L)/(m1+m2)
3) подъем шарика 2
m2*u2^2/2=m2*g*H
H=u2^2/(2*g) =(2*m1*корень(2*g*L)/(m1+m2))^2/(2*g) =
=L*(2*m1/(m1+m2))^2 = 4*L/(1+m2/m1)^2 = 4*0,5/(1+0,3/0,1)^2 = 0,125 м
Похожие вопросы
Предмет: Физика,
автор: mat7280
Предмет: Окружающий мир,
автор: Аноним
Предмет: Литература,
автор: sashachebotarlviv
Предмет: Экономика,
автор: Розka