Предмет: Математика,
автор: reeter
решите неравенство
Приложения:
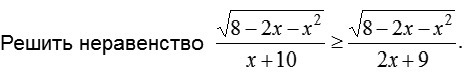
Ответы
Автор ответа:
0
8-2х-х^2>0 , х1 =-4, х2=2. х+10>0, х1=-10. 2х+9>0 х1 =-4,5 хэ[2,+Бесконечности)
Автор ответа:
0
Что за дичь?
Автор ответа:
0
а в чем собственно проблема? одз неверно?
Автор ответа:
0
Ну как тебе сказать. Все что написано - бред. Я вообще не понимаю что ты пытался сделать и зачем.
Автор ответа:
0
можешь пожалуйста показать свое решение, чтоб я понял в чем ошибка и больше не допускал ее.
Автор ответа:
0
Вечерком запощу решение, если больше никто не решит.
Автор ответа:
0
Разбираемся с ОДЗ. Она задается системой
{8-2x-x²≥0
{(x+10)(2x+9)≠0
Решение системы такое: -4≤x≤2
Возвращаемся к неравенству. Корень величина положительная, и на нее можно разделить обе части неравенства перед этим записав его нули x=-4, x=2 (так как знак нестрогий они являются решениями неравенства).
Получаем неравенство:
Которое решается методом интервалов и в пересечение с ОДЗ корня дает решение 1≤x≤2
Ответ: x ∈ {-4} ∪ [1; 2]
Похожие вопросы
Предмет: Английский язык,
автор: lalisamanoban58
Предмет: Математика,
автор: lesya29101992pehm0x
Предмет: Алгебра,
автор: dianaharcenko657
Предмет: Математика,
автор: carolinamelint