Предмет: Математика,
автор: allasokolova6
Найти интерполяционный многочлен Лагранжа P3(x), для которого P3(-1)=-11, P3(1)=-3, P3(3)=13.
Ответы
Автор ответа:
0
Решается система:
Многочлен Лагранжа:
Приложения:
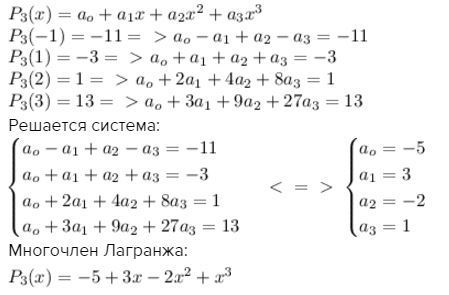
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Русский язык,
автор: dandelionbaby7
Предмет: Русский язык,
автор: Prophisionall
Предмет: Физика,
автор: Heatchliff