Предмет: Алгебра,
автор: masyhjdfutrtd
Помогите решить уравнения!
Приложения:
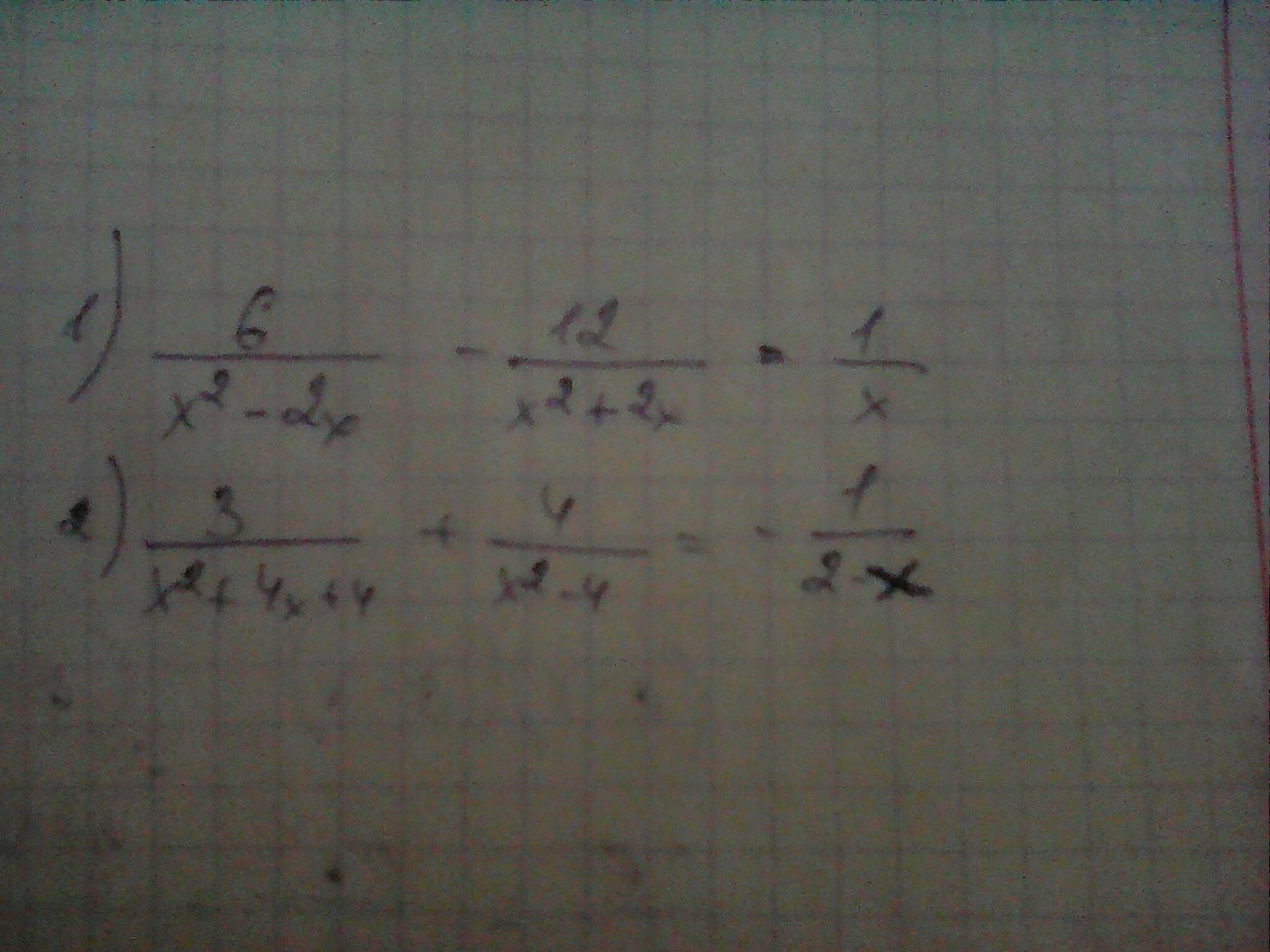
Ответы
Автор ответа:
0
1) ОДЗ: x²+2x≠0 x(x+2)≠0 x≠0
x²-2x≠0 ⇔ x(x-2)≠0 ⇔ x≠2
x≠0 x≠0 x≠-2

x=0 - не удовлетворяет ОДЗ
ОТВ: 4; -10
2) ОДЗ: x²+4x+4≠0 (х+2)²≠0 х≠-2
х²-4≠0 ⇔ (х-2)(х+2)≠0 ⇔ х≠2
2-х≠0 х≠2

х=2 - не удовл. ОДЗ
ОТВ: 1
x²-2x≠0 ⇔ x(x-2)≠0 ⇔ x≠2
x≠0 x≠0 x≠-2
x=0 - не удовлетворяет ОДЗ
ОТВ: 4; -10
2) ОДЗ: x²+4x+4≠0 (х+2)²≠0 х≠-2
х²-4≠0 ⇔ (х-2)(х+2)≠0 ⇔ х≠2
2-х≠0 х≠2
х=2 - не удовл. ОДЗ
ОТВ: 1
Похожие вопросы
Предмет: Математика,
автор: mihailsvir
Предмет: Математика,
автор: rabadanovislam5
Предмет: Математика,
автор: chelovek20000000
Предмет: Математика,
автор: avdalyan62
Предмет: История,
автор: pashi