Предмет: Алгебра,
автор: art123арт
100 баллов!!! Помогите решить и поподробней, пожалуйста!
Приложения:
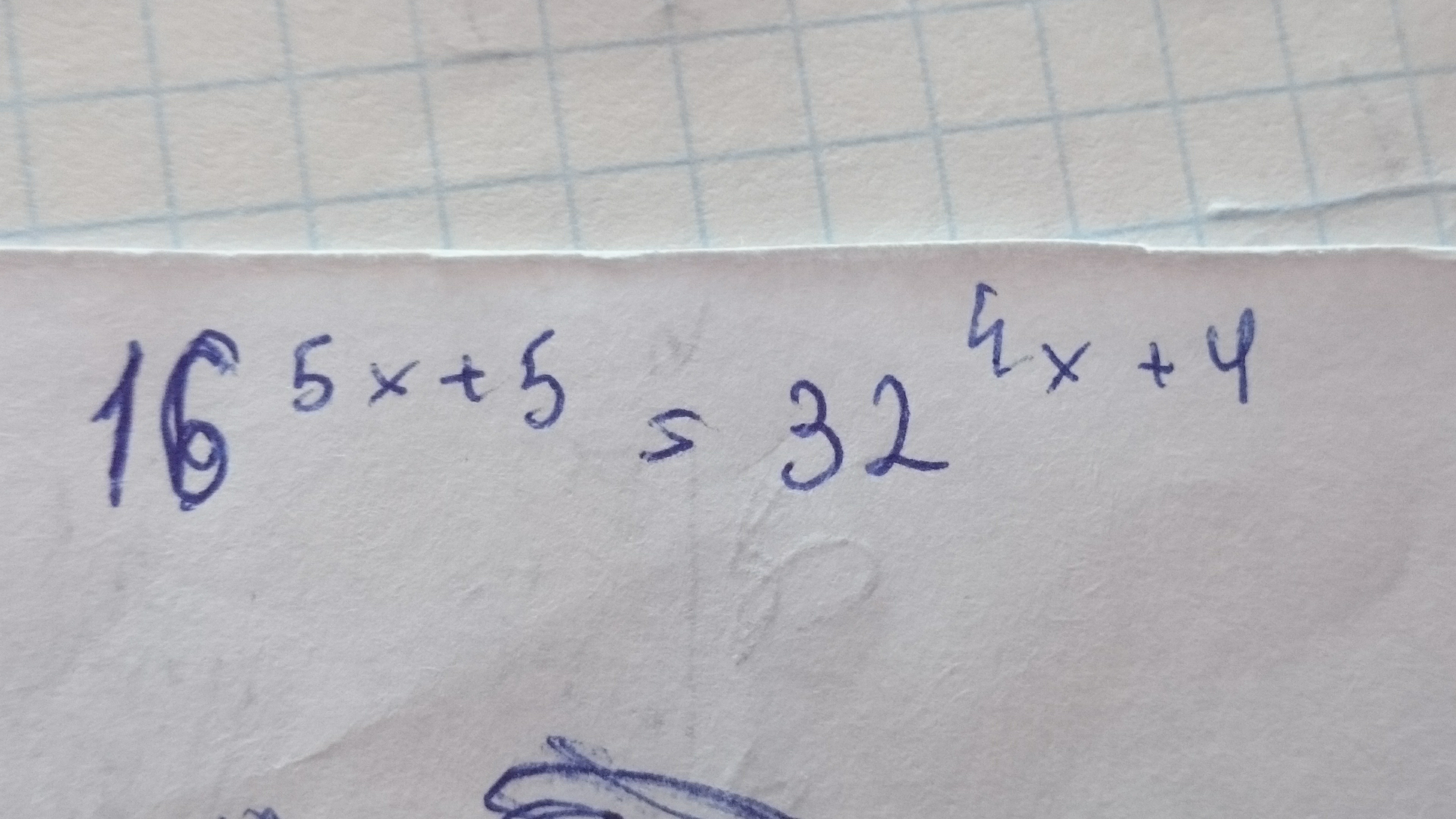
Ответы
Автор ответа:
0
20x+20=20x+20
0=0
Следовательно при любых значениях х уравнение имеет решение
х∈(-∞; +∞)
Автор ответа:
0
Предположим, x=0, тогда 16^5=32^5?
Автор ответа:
0
Ага, ошибся, сорян
Автор ответа:
0
Уходи
Автор ответа:
0
Ой, все
Автор ответа:
0
:-D
Автор ответа:
0
в показательных уравнениях зачастую необходимо свести левую и правую часть к одинаковому основанию (если основания равны, значит приравниваем показатели)
16=4² или 16=2⁴
32=2⁵, значит и 16 и 32 сводим к основанию 2
также понадобится формула :
(aᵇ)ⁿ=aᵇⁿ
переходим к самому уравнению
16⁵ˣ⁺⁵=32⁴ˣ⁺⁴
(2⁴)⁵ˣ⁺⁵=(2⁵)⁴ˣ⁺⁴
2⁴⁽⁵ˣ⁺⁵⁾=2⁵⁽⁴ˣ⁺⁴⁾
2²⁰ˣ⁺²⁰=2²⁰ˣ⁺²⁰
20х+20=20х+20
0=0, следовательно уравнение верно при любых значениях х
х∈(-∞;+∞)
отв:х∈(-∞;+∞)
16=4² или 16=2⁴
32=2⁵, значит и 16 и 32 сводим к основанию 2
также понадобится формула :
(aᵇ)ⁿ=aᵇⁿ
переходим к самому уравнению
16⁵ˣ⁺⁵=32⁴ˣ⁺⁴
(2⁴)⁵ˣ⁺⁵=(2⁵)⁴ˣ⁺⁴
2⁴⁽⁵ˣ⁺⁵⁾=2⁵⁽⁴ˣ⁺⁴⁾
2²⁰ˣ⁺²⁰=2²⁰ˣ⁺²⁰
20х+20=20х+20
0=0, следовательно уравнение верно при любых значениях х
х∈(-∞;+∞)
отв:х∈(-∞;+∞)
Похожие вопросы
Предмет: Математика,
автор: karpenkoviktoria861
Предмет: Математика,
автор: karpenkoviktoria861
Предмет: География,
автор: Аноним
Предмет: Алгебра,
автор: kimy98