Предмет: Математика,
автор: Violettatremor
Привести уравнение кривой второго порядка f(х;у)=0 к каноническому виду и найти точки пересечения ее с прямой Ах+Ву+С=0.Выполните графическую иллюстрацию
полученного решения.
2x^2-4x-y+3+0; 2x-y-1=0
Ответы
Автор ответа:
0
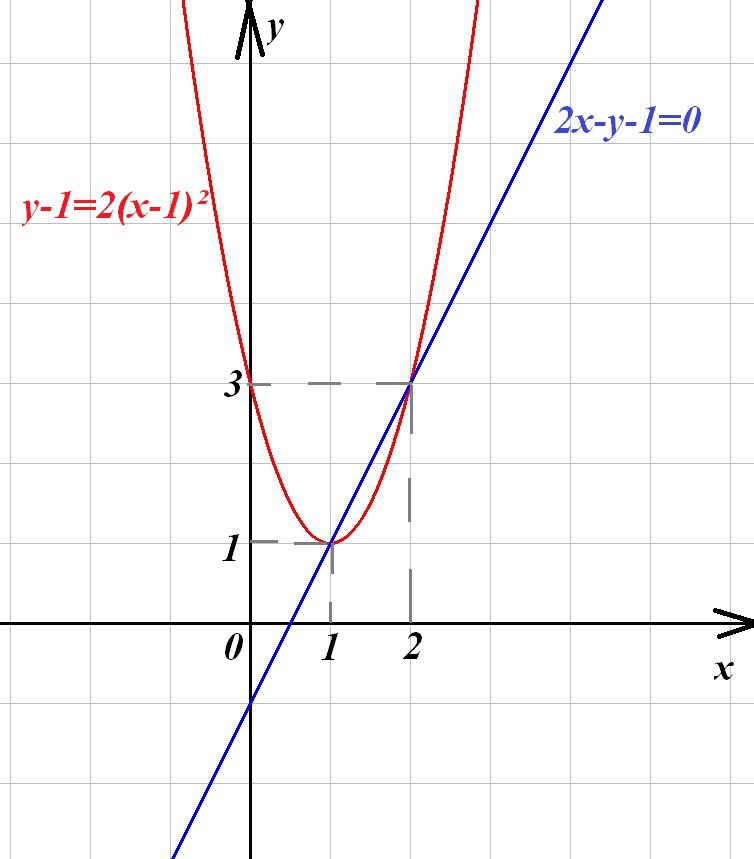
Получили уравнение параболы с вершиной в точке (1;1) и ветвями, направленными вверх. х=1 - ось симметрии параболы.
Найдем точки пересечения линий:
(1;1) и (2;3) - точки пересечения параболы и прямой.
Иллюстрация - во вложении
Приложения:
Похожие вопросы
Предмет: Математика,
автор: alena10gavrilina
Предмет: Русский язык,
автор: vakadypa13
Предмет: Литература,
автор: kusya228
Предмет: Биология,
автор: rlit2013
Предмет: История,
автор: Аноним