Предмет: Математика,
автор: пирожок8
как решить это уравнение?
Приложения:
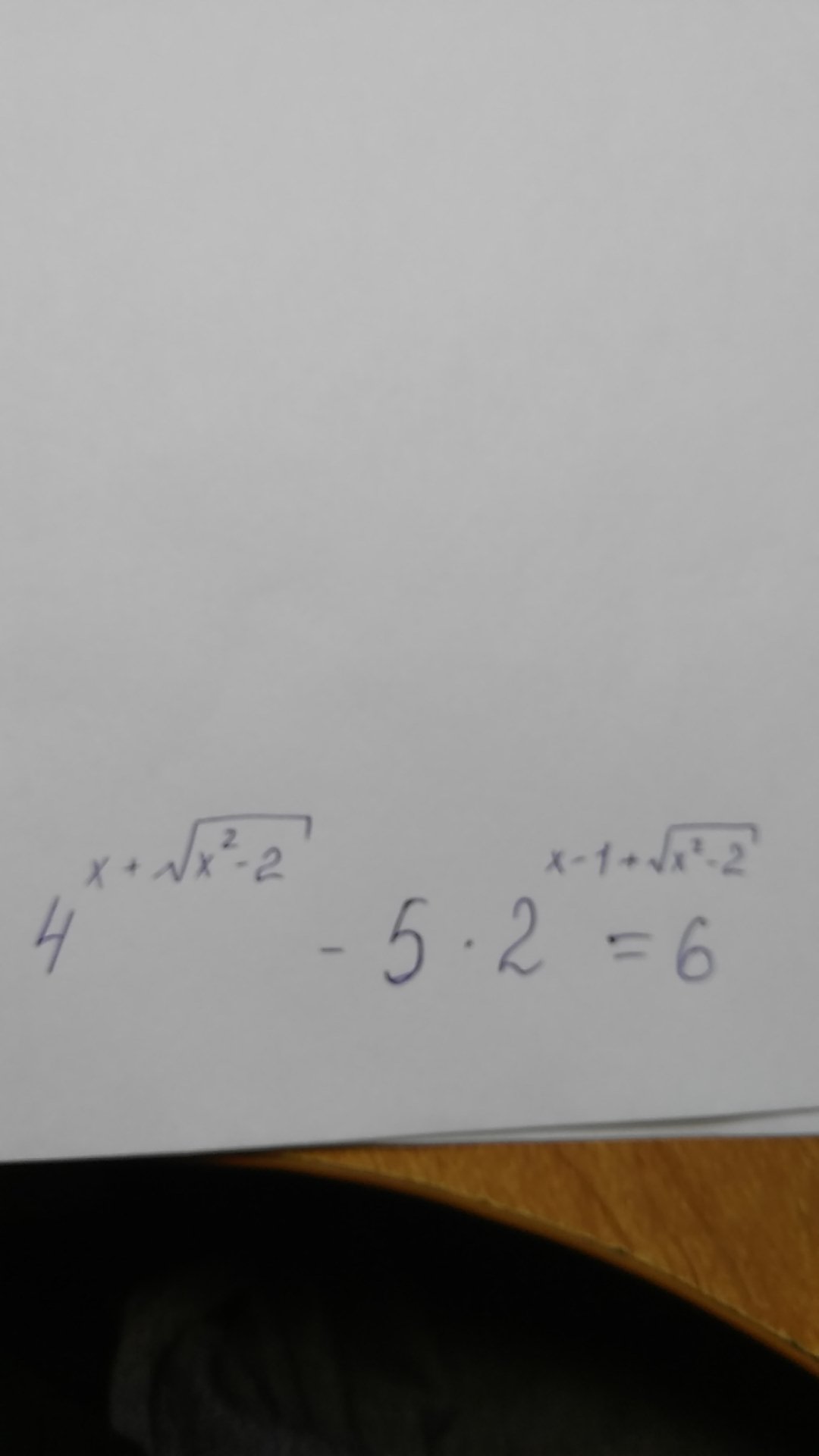
Ответы
Автор ответа:
0
Автор ответа:
0
в уравнении есть корень квадратный, значит найдем ОДЗ:
х²-2≥0
(х-√2)(х+√2)≥0
х≥√2 или х≤√2
теперь переходим к самому уравнению.

 -не удовлетворяет условию t>0
-не удовлетворяет условию t>0

ОТВЕТ: 1,5
х²-2≥0
(х-√2)(х+√2)≥0
х≥√2 или х≤√2
теперь переходим к самому уравнению.
ОТВЕТ: 1,5
Автор ответа:
0
спасибо большое
Похожие вопросы
Предмет: Химия,
автор: PR0BIRKA
Предмет: Химия,
автор: adv1142
Предмет: Математика,
автор: denisgavrilisen1
Предмет: Математика,
автор: sazonovalusi
Предмет: Информатика,
автор: lalalaoooll