Предмет: Математика,
автор: ZiXMaX
Указать какому промежутку принадлежит сумма корней уравнения: 7x^2-3-15=0
Ответы
Автор ответа:
0
Там где 3 ты потерял х, только в том случае мы получаем дискриминант. У меня не получается извлечь корень, он не извлекается. А вот промежутки я написал и на числовой прямой указал.
Приложения:
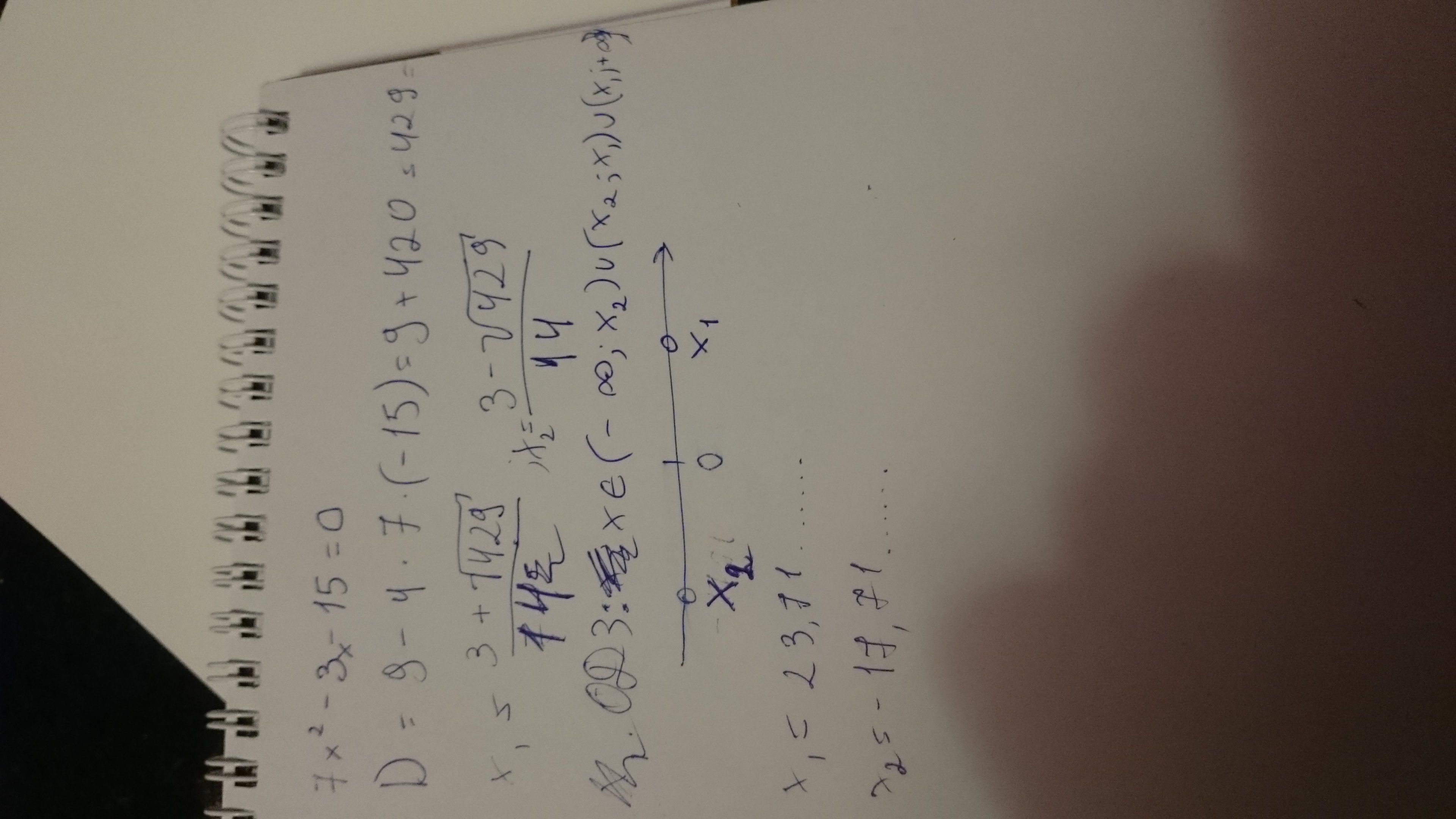
Автор ответа:
0
Как полагаю я, перед моими глазами не уравнение вида  , а квадратное. Посоветовал бы для начала умножить все части уравнения на –1, получив при этом уравнение вида
, а квадратное. Посоветовал бы для начала умножить все части уравнения на –1, получив при этом уравнение вида  , уже легче поддающееся решению.
, уже легче поддающееся решению.
 , или равен
, или равен  , что в калькуляторе равно примерно 20,712...
, что в калькуляторе равно примерно 20,712...
Дискриминант мы сосчитали – равен он квадратному корню из четыреста двадцати девяти, а вот корни уравнения мы ещё не сосчитали. Займёмся этим.

Счесть корни фактически невозможно, печаль. Сумма корней уравнения (а иначе ) расписывается следующим образом (конкретно для данного уравнения):
) расписывается следующим образом (конкретно для данного уравнения):
 и равна она, вообщем-то, шести четырнадцатым – обозначим её переменной α. Теперь же начертим числовую прямую, обозначив на ней α.
и равна она, вообщем-то, шести четырнадцатым – обозначим её переменной α. Теперь же начертим числовую прямую, обозначив на ней α.
\\\\0/////α///
––––––|–––––––>
где , или равно
, или равно  .
.
Тогда промежуток, принадлежащий этому значения, имеет следующий вид:
x∈(–∞; α)∪(α; +∞), ну либо x∈(–∞; )∪(
)∪( ; +∞)
; +∞)
Дискриминант мы сосчитали – равен он квадратному корню из четыреста двадцати девяти, а вот корни уравнения мы ещё не сосчитали. Займёмся этим.
Счесть корни фактически невозможно, печаль. Сумма корней уравнения (а иначе
\\\\0/////α///
––––––|–––––––>
где
Тогда промежуток, принадлежащий этому значения, имеет следующий вид:
x∈(–∞; α)∪(α; +∞), ну либо x∈(–∞;
Приложения:
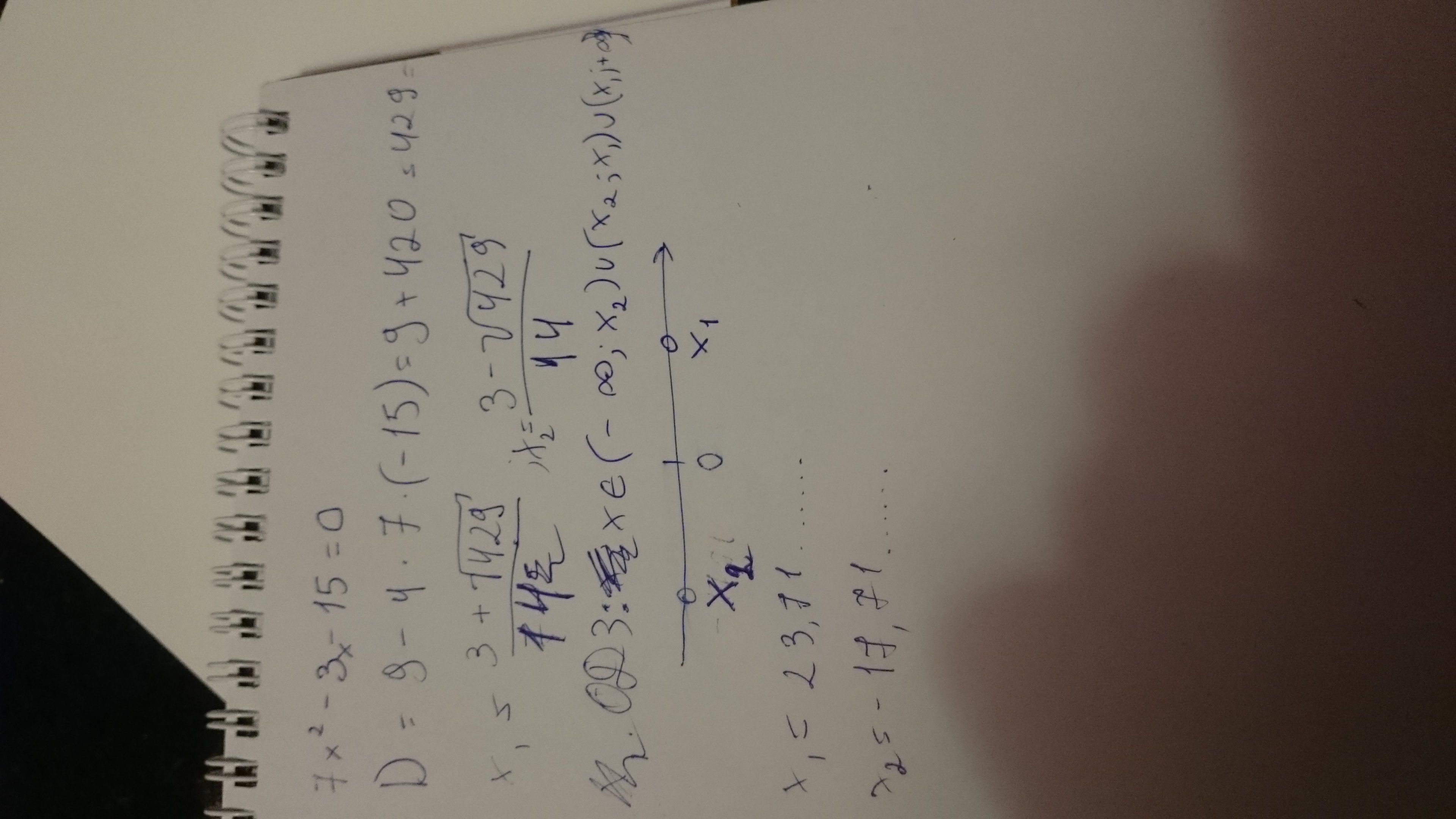
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Українська література,
автор: streamtim19
Предмет: Алгебра,
автор: rostislavvv77
Предмет: Математика,
автор: Диана190
Предмет: Математика,
автор: sofiya3009