Предмет: Математика,
автор: nas1234987
С подробным решением, пожалуйста
Приложения:
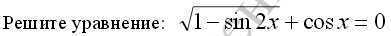
Ответы
Автор ответа:
0
√(1-sin2x)+cosx=0
так как √(1-sin2x)≥0, то cosx ≤0.
учтем, что sin²x+cos²x=1
и что sin2x=2sinx cosx
√(sin²x+cos²x-2sinxcosx)+cosx=0
√(sinx-cosx)²+cosx=0
sinx-cosx+cosx=0
sinx=0
x= пn, где n= 0, ±1, ±2...
учитывая, что cosx ≤0, то
x= п+2пn=п(1+2n), где n= 0, ±1, ±2..
так как √(1-sin2x)≥0, то cosx ≤0.
учтем, что sin²x+cos²x=1
и что sin2x=2sinx cosx
√(sin²x+cos²x-2sinxcosx)+cosx=0
√(sinx-cosx)²+cosx=0
sinx-cosx+cosx=0
sinx=0
x= пn, где n= 0, ±1, ±2...
учитывая, что cosx ≤0, то
x= п+2пn=п(1+2n), где n= 0, ±1, ±2..
Похожие вопросы
Предмет: Другие предметы,
автор: Dasha200125лилмик
Предмет: Математика,
автор: finogeevnik10
Предмет: Математика,
автор: valerevicpavel288
Предмет: Алгебра,
автор: dinaramuzafaro2
Предмет: Геометрия,
автор: vikaivanova19