Question

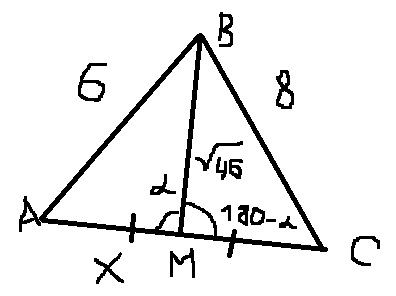
стороны треугольника равны 6 см и 8 см. Медиана треугольника, проведена к его третьей стороне, равна ^46 см. Найдите неизвестную сторону

Answer 1

Придется воспользоваться теоремой косинусов.

Смотри рисунок. Обозначим BM - медиана, AM=x см,

$angle BMA =alpha</var>, quad <var>angle BMC =180^0-alpha</var>$</p> <p> </p> <p>Выразим АВ по теореме косинусов через треугольник АВМ.</p> <p><img src=[/tex]AB^2=BM^2+AM^2-2*BM*AM*cosalpha" title="angle BMA =alpha, quad angle BMC =180^0-alpha " title="AB^2=BM^2+AM^2-2*BM*AM*cosalpha" title="angle BMA =alpha, quad angle BMC =180^0-alpha " alt="AB^2=BM^2+AM^2-2*BM*AM*cosalpha" title="angle BMA =alpha, quad angle BMC =180^0-alpha " />

 

Выразим АВ по теореме косинусов через треугольник АВМ.

$angle BMA =alpha</var>, quad <var>angle BMC =180^0-alpha</var>$

 

Выразим АВ по теореме косинусов через треугольник АВМ.

$<var>AB^2=BM^2 AM^2-2*BM*AM*cosalpha$

 

$36=46 x^2-2*x*sqrt{46}*cosalpha</var>quad (1)$

 

$<var>AB^2=BM^2+AM^2-2*BM*AM*cosalpha$

 

$36=46 x^2-2*x*sqrt{46}*cosalpha</var>quad (1)$

 

Выразим ВC по теореме косинусов через треугольник ВCМ.

 

$<var>BC^2=BM^2+CM^2-2*BM*CM*cos(180^0-alpha)$

 

Выразим ВC по теореме косинусов через треугольник ВCМ.

 

$36=46+x^2-2*x*sqrt{46}*cosalpha</var>quad (1)$

 

Выразим ВC по теореме косинусов через треугольник ВCМ.

 

$<var>BC^2=BM^2 CM^2-2*BM*CM*cos(180^0-alpha)$

 

$64=46+x^2-2*sqrt{46}*x*(cos180^0cosalpha+sin180^0sinalpha)$

 

$64=46+x^2-2*sqrt{46}*x*(-cosalpha)$

 

$64=46 x^2 2*sqrt{46}*x*cosalpha</var>quad(2)$

 

$64=46+x^2-2*sqrt{46}*x*(cos180^0cosalpha+sin180^0sinalpha)$

 

$64=46+x^2-2*sqrt{46}*x*(-cosalpha)$

 

$<var>BC^2=BM^2+CM^2-2*BM*CM*cos(180^0-alpha)$

 

$64=46+x^2-2*sqrt{46}*x*(cos180^0cosalpha+sin180^0sinalpha)$

 

$64=46+x^2-2*sqrt{46}*x*(-cosalpha)$

 

$64=46 x^2 2*sqrt{46}*x*cosalpha</var>quad(2)$

 

Составим систему уравнений из (1) и (2)

 

$<var>left { {{36=46+x^2-2*x*sqrt{46}*cosalpha} atop {64=46+x^2+2*x*sqrt{46}*cosalpha}} right.$

 

Составим систему уравнений из (1) и (2)

 

$64=46+x^2+2*sqrt{46}*x*cosalpha</var>quad(2)$

 

Составим систему уравнений из (1) и (2)

 

$<var>left { {{36=46+x^2-2*x*sqrt{46}*cosalpha} atop {64=46+x^2+2*x*sqrt{46}*cosalpha}} right. " /></var></p> <p> </p> <p>Нам нужно найти x. Поэтому надо избавиться от второго неизвестного. Поступим следующим образом. Вычтем из второго уравнения первое и выразим слагаемое с переменной альфа.</p> <p> </p> <p>[tex]4*x*sqrt{46}*cosalpha=64-36$

 

$4*x*sqrt{46}*cosalpha=28$

 

$2*x*sqrt{46}*cosalpha=14$

 

Теперь подставим верхнее значение слагаемого с альфа в первое уравнение системы

 

$36=46+x^2-14$

 

$36=x^2+32$

 

$x^2=4$

 

x=2.

 

Значит

 

АС=2*х

АС=2*2

АС=4

 

Ответ: 4