Question

помогите плиз в сделать!

Answer 1

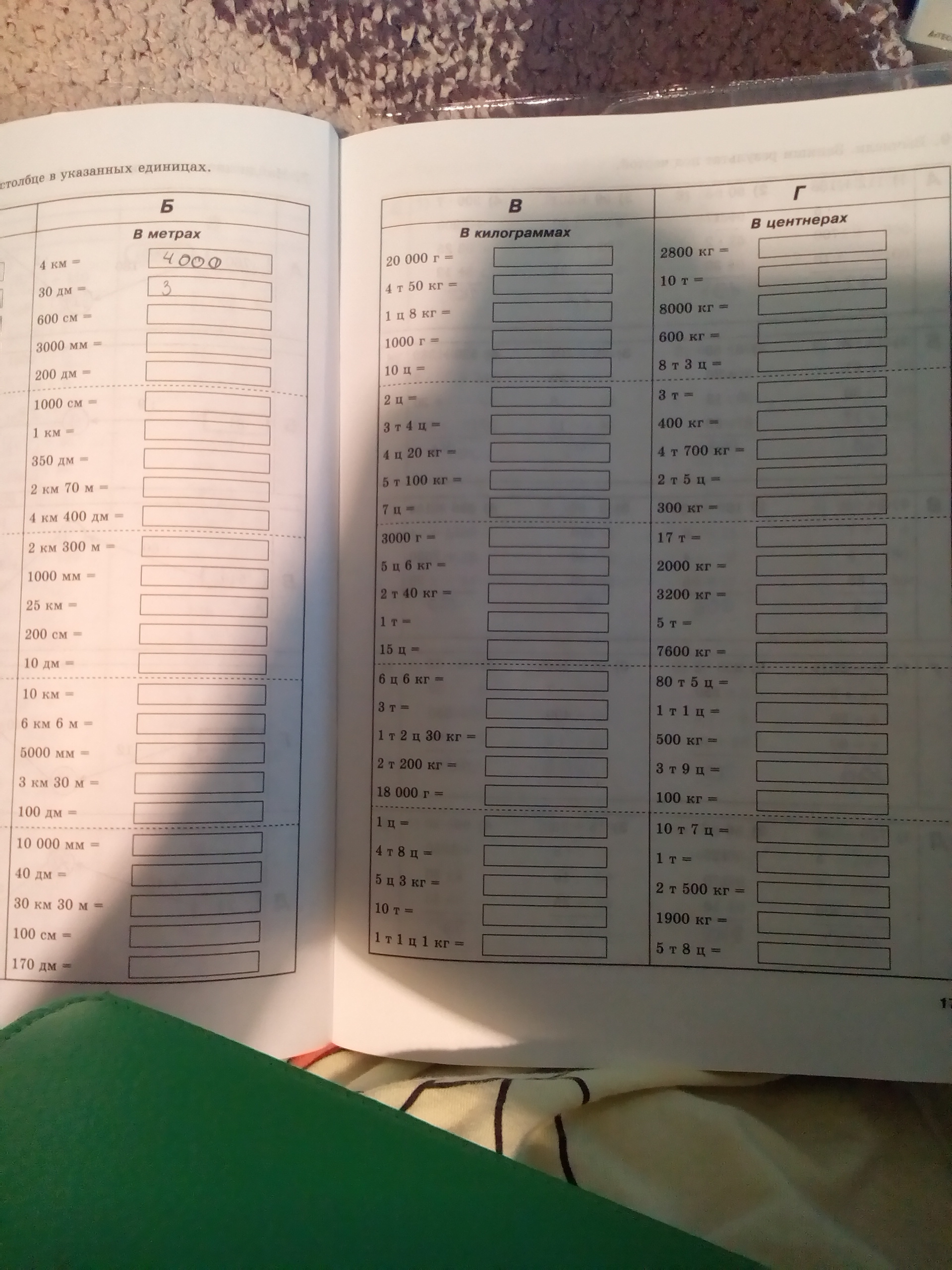
20 000 г=20 кг (1 кг=1000 г).
4 т 50 кг=4050 кг (1 т=1000 кг).
1 ц 8 кг=108 кг (1 ц=100 кг).
1000 г=1 кг.
10 ц=1000 кг.
2 ц= 200 кг.
3 т 4 ц=3 400 кг
4 ц 20 кг=420 кг.
5 т 100 кг= 5100 кг.
7 ц=700 кг.
3000 г=3 кг.
5 ц 6 кг=506 кг.
2 т 40 кг=2040 кг.
1 т=1000 кг.
15 ц=1500 кг.
6 ц 6кг=606 кг.
3 т=3000 кг.
1 т 2 ц 30 кг=1230 кг.
2 т 200 кг=2 200 кг.
18 000 г=18 кг.
1 ц=100 кг.
4 т 8 ц=4800 кг.
5 ц 8 кг=5008 кг.
10 т=10 000 кг.
1 т 1 ц 1 кг=1101 кг.