Question

найти площадь фигуры ограниченной линиями yx=3, y+x=4

Answer 1

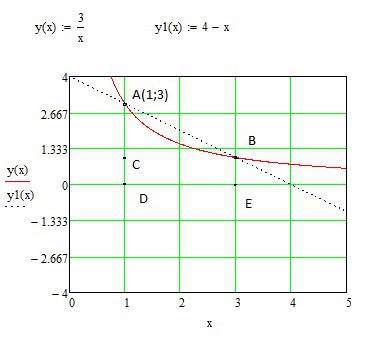
Площадь фигуры AB (ограниченная двумя линиями) считаем как Sab=Sabde-Sabc, здесь Sabc=интеграл от 1 до 3 (3/x)dx=3,296 кв. единиц (от красной сплошной линии). S abde=Scbde+Sabc (от пунктирной линии). Scbde=1*2=2 кв. единицы (пл-дь прямоугольника)
Sabc=2*2/2=2 кв. единицы (пл-дь треугольника). Sabde=2+2=4 в. единицы. Sab=4-3,296= 0,704 кв. единицы.