Предмет: Геометрия,
автор: Asiia
перпендикуляр, опущенный из вершины тупого угла ромба на его сторону, делит большую диагональ на отрезки, равные 3,5 см и 12,5 см. Определить сторону и меньшую диагональ ромба.
Ответы
Автор ответа:
0
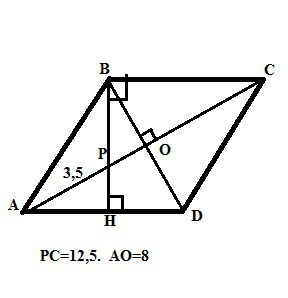
Дан ромб АВСD. Точка О - точка пересечения его диагоналей. Точка Р - точка пересечения перпендикуляра ВН (высоты ромба) и большей диагонали АС.
В ромбе диагонали взаимно перпендикулярны и точкой пересечения делятся пополам. Большая диагональ ромба равна сумме данных нам отрезков: 3,5+12,5=16см. Половина ее равна 8см. В прямоугольном треугольнике РВС (<PBC=90°, дано) ВО - высота из прямого угла и по свойствам этой высоты равна ВО=√(РО*ОС). ОС=8 (половина диагонали), РО=АО-АР=8-3,5=4,5. Тогда ВО=√(4,5*8)=√(9*4)=6см.
ВО - это половина меньшей диагонали. Значит меньшая диагональ равна 12см. Сторона ромба АВ найдется из прямоугольного треугольника АОВ по Пифагору: АВ=√(АО²+ВО²)=√(64+36)=10см.
Ответ: сторона ромба равна 10см, его меньшая диагональ равна 12см.
В ромбе диагонали взаимно перпендикулярны и точкой пересечения делятся пополам. Большая диагональ ромба равна сумме данных нам отрезков: 3,5+12,5=16см. Половина ее равна 8см. В прямоугольном треугольнике РВС (<PBC=90°, дано) ВО - высота из прямого угла и по свойствам этой высоты равна ВО=√(РО*ОС). ОС=8 (половина диагонали), РО=АО-АР=8-3,5=4,5. Тогда ВО=√(4,5*8)=√(9*4)=6см.
ВО - это половина меньшей диагонали. Значит меньшая диагональ равна 12см. Сторона ромба АВ найдется из прямоугольного треугольника АОВ по Пифагору: АВ=√(АО²+ВО²)=√(64+36)=10см.
Ответ: сторона ромба равна 10см, его меньшая диагональ равна 12см.
Приложения:
Похожие вопросы
Предмет: Химия,
автор: BAKALCHUKIVANNA
Предмет: Алгебра,
автор: sinelnikantonina2006
Предмет: Английский язык,
автор: babkaperdunia
Предмет: Химия,
автор: Florai