Предмет: Математика,
автор: mayskayaelzave
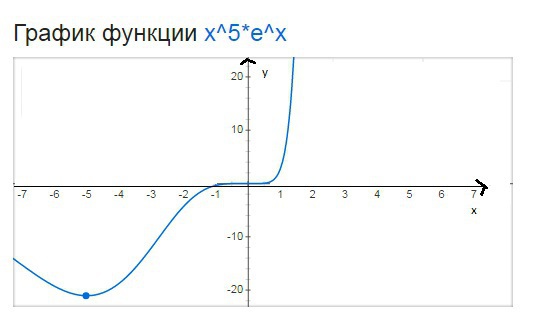
Найдите точку минимума функции f(x)=x^5*e^x+1
Ответы
Автор ответа:
0
y'=5x^4e^x+x^5e^x=0
(x^4)(e^x)(5+x)=0
1) x=0
2) x=-5
при x<-5, y'<0, у убывает
при -5<х, y'>0, у возрастает
⇒ при х=-5 минимум
у(-5)=(-5)^5*((e^(-5)+1=(-3125/(e^5))+1
(-5, -3125e^5+1) - точка минимума
график на картинке
(x^4)(e^x)(5+x)=0
1) x=0
2) x=-5
при x<-5, y'<0, у убывает
при -5<х, y'>0, у возрастает
⇒ при х=-5 минимум
у(-5)=(-5)^5*((e^(-5)+1=(-3125/(e^5))+1
(-5, -3125e^5+1) - точка минимума
график на картинке
Приложения:
Похожие вопросы
Предмет: Математика,
автор: flipperflapper
Предмет: Математика,
автор: Ebatka
Предмет: Геометрия,
автор: yaroslavyefymovych
Предмет: Биология,
автор: byloslovo