Question

напишите уравнение касательной к графику функции y=6x^2+5x в точке x0=2

Answer 1

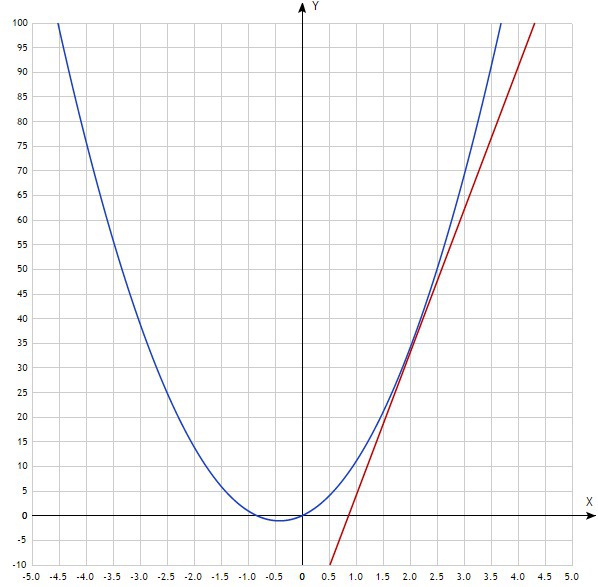
Уравнение касательной имеет вид
y=f(x₀)+f'(x₀)(x-x₀)
x₀=2
f(2)=6*2²+5*2=24+10=34
Найдём производную функции
f'(x)=(6x²+5x)'=12x+5
А теперь значение производной в точке х₀:
f'(2)=12*2+5=29
Подставляем найденные значения в формулу касательной:
y=34+29(x-2)=34+29x-58=29x-25