Предмет: Математика,
автор: Lolkaok
помогите решить (y+1)dx=2dxy при x=4,y=1
Приложения:
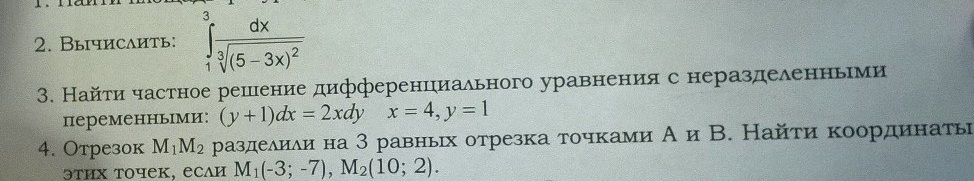
Ответы
Автор ответа:
0
(y+1)dx=2хdy=это ДУ с разделяющимися переменными.
Имеем 2dy/(y+1)=dx/x. Интегрируем обе части по х:
2∫dy/(y+1)=∫dx/x
2Ln(y+1)=Lnx+LnC, Lny²=LnCx или у²=Сх.
При х=4 и у=1 имеем:4С=1 и С=0.25 и тогда имеем ч.р.
у²=0.25х
Имеем 2dy/(y+1)=dx/x. Интегрируем обе части по х:
2∫dy/(y+1)=∫dx/x
2Ln(y+1)=Lnx+LnC, Lny²=LnCx или у²=Сх.
При х=4 и у=1 имеем:4С=1 и С=0.25 и тогда имеем ч.р.
у²=0.25х
Похожие вопросы
Предмет: Математика,
автор: alinarazskih32
Предмет: Русский язык,
автор: ipronin995
Предмет: Экономика,
автор: nastyayureva290
Предмет: Химия,
автор: xXxXAlinaXxXx