Предмет: Математика,
автор: kulikoff32452
Решить определенный интеграл
Задание 4 (в,г)
Приложения:
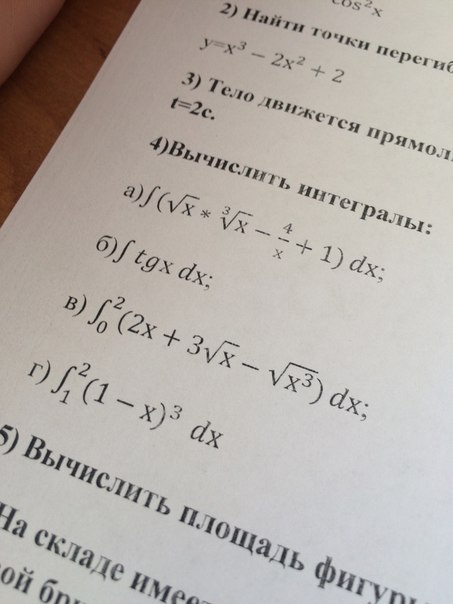
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Геометрия,
автор: Аноним
Предмет: Математика,
автор: valamalceva37217
Предмет: Литература,
автор: fedorkobov99305
Предмет: Алгебра,
автор: diulin