Question

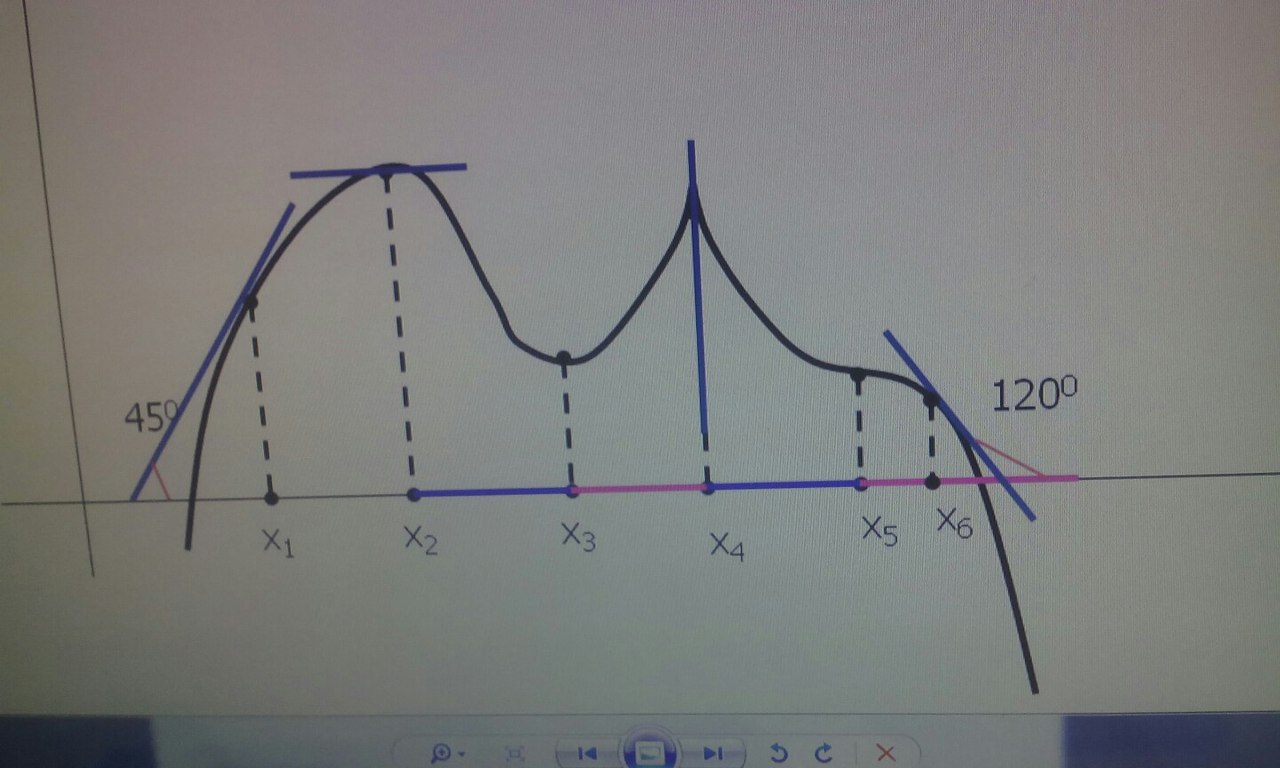
Найти производные в точках х1, х2, х4 и х6. Указать знак производной на интервалах [x2, x3], [x3, x4]. Указать знак второй производной на интеровале [x4, x5], [x5, x6]. Указать критические точки, точки экстремумов

Answer 1

f'(x1)=tg45°=1
f'(x2)=tg0°=0,
f'(x3)=tg0°=0,
f'(x4)- не существует производная
f'(x5)=tg0°=0,
f'(x6)=tg120°=tg(180°- 60°)=- tg60°=-√3
f'(x)<0, на [x2; x3], функция f(x) - убывает, f'(x)>0, на проме.жутке [x3; x4], функция на этом промежутке возрастает.
на [х4;х5], f"(x)>0, т.к. функция на этом промежутке выпукла вниз.
на промежутке [x5; x6], f"(x)<0, функция выпукла вверх.
Критические точки: х2, х3, х4
Точки экстремума: х2- точка максимума, х3 - точка минимума, х4 - точка максимума