Предмет: Физика,
автор: stalkerdryg
1. Даны уравнения движения двух тел: X1= t2-6t+16 и X2= 10t-7
Используя уравнения движения каждого тела определить 1) вид движения каждого тела; 2) начальные координаты, величину и направление начальной скорости; 3) сделать чертеж вдоль оси ОХ; 4)определить модуль и направление ускорения; 5) найти место и время встречи тел; построить графики для каждого тела.
Помогите решить темы совсем не понимаю((((((
Ответы
Автор ответа:
0
x1(t) = t² - 6t + 16
x2(t) = 10t - 7
прежде чем отвечать на вопросы, я предоставлю вам краткую теорию
во-первых, для решения данной задачи нужно знать зависимость координаты от времени при равноускоренном (равнопеременном) прямолинейном движении и при равномерном прямолинейном движении
при равноускор. прям. движ.: x(t) = x0 + v0x*t + (a(x) t²)/2
при равном. прям. движ.: x(t) = x0 + v0x*t
вы можете заметить, что зависимости в задаче x(t) даны "наоборот", а поэтому целесообразно их переписать в следующем виде:
x1(t) = 16 - 6t + t²
x2(t) = -7 + 10t
теперь приступим к решению вопросов
1.
x1(t) - равноускоренное (равнопеременное) прямолинейное движение
x2(t) - равномерное прямолинейное движение
2.
смотря на приведенные выше уравнения зависимости x(t), определяем:
1 тело: x0 = 16 м, |v0x| = 6 (не сонаправлена с осью абсцисс)
2 тело: x0 = -7 м, |v0x| = 10 (сонаправлена с осью абсцисс)
3.
это задание, вероятно, предполагает схематичное изображение графиков зависимостей x(t) вдоль оси абсцисс, а потому достаточно для 1 тела нарисовать параболу (ветви вверх), а для второго - прямую (направленную по направлению оси абсцисс)
4.
аналогично 2 заданию, определяем:
для 1 тела: |a(x)| = 2 м/с^2 (направление сонаправлено с осью абсцисс)
для 2 тела: |a(x)| = 0
5.
1) ясно, что в момент встречи у тел одинаковая координата X
то есть, x1 = x2. приравняв уравнения и приведя подобные, решим квадратное уравнение и найдем время встречи:
t² - 16t + 23 = 0.
t1 = 14,4 c; t2 = 1,6 c
для координат встречи достаточно подставить значения t1 и t2 в любое из уравнений. подставим, например, в x2(t). тогда находим координаты встречи:
x1 = 137 м; x2 = 9 м
2) теперь построим графики зависимости x(t) для обоих тел
в случае с x2(t) все довольно просто, достаточно соединить точки встречи тел (x1;t1) и (x2;t2)
в случае с x1(t) необходимо найти вершину параболы. она ищется по формуле x = -b / 2a (ордината находится подстановкой значения x в уравнение функции)
относительно наших координат находим, что x = 7 м, t = 3 c
теперь достаточно продолжить ветви параболы к точкам встречи. если вам нужен более подробный график, то целесообразно уточнить параболу по дополнительным точкам
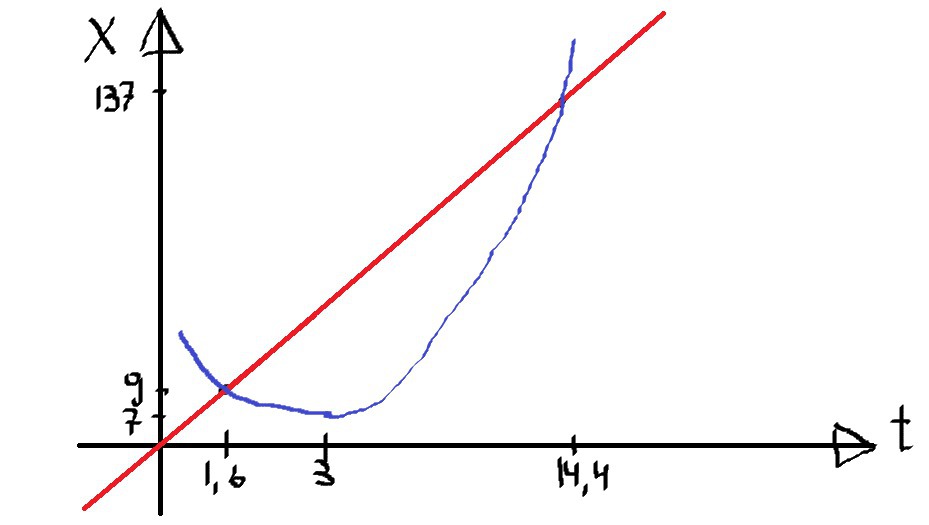
схематичное изображение того, что должно получиться, представлено в приложении
x2(t) = 10t - 7
прежде чем отвечать на вопросы, я предоставлю вам краткую теорию
во-первых, для решения данной задачи нужно знать зависимость координаты от времени при равноускоренном (равнопеременном) прямолинейном движении и при равномерном прямолинейном движении
при равноускор. прям. движ.: x(t) = x0 + v0x*t + (a(x) t²)/2
при равном. прям. движ.: x(t) = x0 + v0x*t
вы можете заметить, что зависимости в задаче x(t) даны "наоборот", а поэтому целесообразно их переписать в следующем виде:
x1(t) = 16 - 6t + t²
x2(t) = -7 + 10t
теперь приступим к решению вопросов
1.
x1(t) - равноускоренное (равнопеременное) прямолинейное движение
x2(t) - равномерное прямолинейное движение
2.
смотря на приведенные выше уравнения зависимости x(t), определяем:
1 тело: x0 = 16 м, |v0x| = 6 (не сонаправлена с осью абсцисс)
2 тело: x0 = -7 м, |v0x| = 10 (сонаправлена с осью абсцисс)
3.
это задание, вероятно, предполагает схематичное изображение графиков зависимостей x(t) вдоль оси абсцисс, а потому достаточно для 1 тела нарисовать параболу (ветви вверх), а для второго - прямую (направленную по направлению оси абсцисс)
4.
аналогично 2 заданию, определяем:
для 1 тела: |a(x)| = 2 м/с^2 (направление сонаправлено с осью абсцисс)
для 2 тела: |a(x)| = 0
5.
1) ясно, что в момент встречи у тел одинаковая координата X
то есть, x1 = x2. приравняв уравнения и приведя подобные, решим квадратное уравнение и найдем время встречи:
t² - 16t + 23 = 0.
t1 = 14,4 c; t2 = 1,6 c
для координат встречи достаточно подставить значения t1 и t2 в любое из уравнений. подставим, например, в x2(t). тогда находим координаты встречи:
x1 = 137 м; x2 = 9 м
2) теперь построим графики зависимости x(t) для обоих тел
в случае с x2(t) все довольно просто, достаточно соединить точки встречи тел (x1;t1) и (x2;t2)
в случае с x1(t) необходимо найти вершину параболы. она ищется по формуле x = -b / 2a (ордината находится подстановкой значения x в уравнение функции)
относительно наших координат находим, что x = 7 м, t = 3 c
теперь достаточно продолжить ветви параболы к точкам встречи. если вам нужен более подробный график, то целесообразно уточнить параболу по дополнительным точкам
схематичное изображение того, что должно получиться, представлено в приложении
Приложения:
Автор ответа:
0
Невероятно супер просто супер огроменное спасибо!
Похожие вопросы