Предмет: Математика,
автор: KSeH9
Определить сходимость рядов:
Приложения:
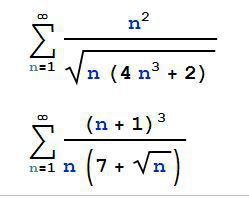
Ответы
Автор ответа:
0
оба ряда сходятся по следствию из необходимого признака сходимости, который звучит так: если lim an≠0 при n⇒∞, то ряд числовой расходится.
У нас в первом ряде lim n^2/√n(4n^3+2)=1/√(4+2/n^3)=1/2 ≠0 при n⇒∞. мы здесь числитель и знаменатель разделили на n^2
Во втором ряде lim an=(∞/∞) по правилу Лопиталя = lim (n+1)^2/1/(2√n)=
lim2√n·(n+1)^2 = ∞ ≠ 0, ⇒ряд расходится
У нас в первом ряде lim n^2/√n(4n^3+2)=1/√(4+2/n^3)=1/2 ≠0 при n⇒∞. мы здесь числитель и знаменатель разделили на n^2
Во втором ряде lim an=(∞/∞) по правилу Лопиталя = lim (n+1)^2/1/(2√n)=
lim2√n·(n+1)^2 = ∞ ≠ 0, ⇒ряд расходится
Похожие вопросы
Предмет: История,
автор: noname30011945
Предмет: Українська мова,
автор: alyaji0497
Предмет: Математика,
автор: shamans32858
Предмет: Экономика,
автор: vivatstarko