Предмет: Математика,
автор: okhachov
Помогите решить интеграл
Приложения:
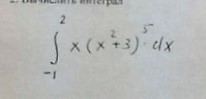
Ответы
Автор ответа:
0
Автор ответа:
0
Произведём замену.
x^2 + 3 = t
Тогда
2xdx = dt => xdx = dt/2
Также заменим пределы интегрирования.
x | t
2 | 5
-1 | 4
Интеграл принимает вид: по пределам 7 и 4.
по пределам 7 и 4.
Вычислив полученное по формуле Ньютона-Лейбница, получим:
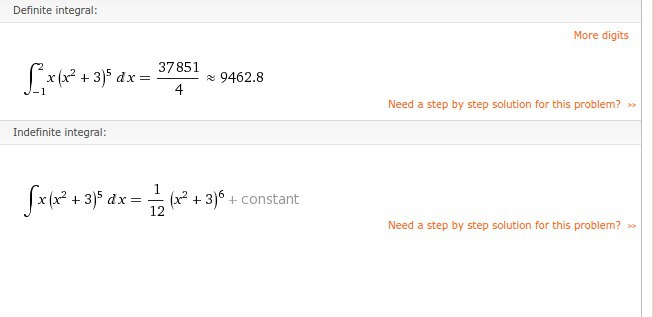
ответ: 37851/4 или же 9462,75
Пруф на картинке.
x^2 + 3 = t
Тогда
2xdx = dt => xdx = dt/2
Также заменим пределы интегрирования.
x | t
2 | 5
-1 | 4
Интеграл принимает вид:
Вычислив полученное по формуле Ньютона-Лейбница, получим:
ответ: 37851/4 или же 9462,75
Пруф на картинке.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: alinakravchenko3107
Предмет: Французский язык,
автор: bgg133
Предмет: Физика,
автор: dmytromartun
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: ЕваВикторовна