Предмет: Математика,
автор: katavagner
Почему в ответе получается {-4} u [2;3]. То что [2;3] входит в ответ, это понятно, но почему в ответ входит точка -4?
Приложения:
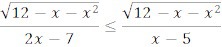
Ответы
Автор ответа:
0
еще в числителе подкоренное выражение должно быть больше 0, если решим его получатся два корня 3 и -4
Автор ответа:
0
В числителе подкоренное выражение должно быть больше или равно нулю.
Автор ответа:
0
подкоренное выражение всегда больше 0
Автор ответа:
0
Подкоренное выражение всегда НЕОТРИЦАТЕЛЬНО, то есть больше или равно нулю !!! Из-за этого та самая (-4) и входит в ответ.
Автор ответа:
0
очень хорошее решение вам написал NNNLLL54
Автор ответа:
0
Квадратный корень всегда неотрицателен, то есть положителен или равен нулю, значит на знак неравенства не повлияет.
Но так как корень может быть = 0 и он присутствует в числителе, а знак неравенства нестрогий (равенство нулю допускается), то надо учесть при решении неравенства , что точки х=-4 и х=3 могут входить в решение.
Автор ответа:
0
Спасибо большое! Я понял где -4 потерял
Похожие вопросы
Предмет: Математика,
автор: sadfaFSDgsd
Предмет: Русский язык,
автор: Sevda2009
Предмет: Алгебра,
автор: dfsfsdf3254324
Предмет: География,
автор: ritulay2002
Предмет: Математика,
автор: juliamaxuta