Предмет: Математика,
автор: dimon189
Надо решить 4-е задание и по возможности 3-е
Помогите пожалуйста
заранее благодарен
Приложения:
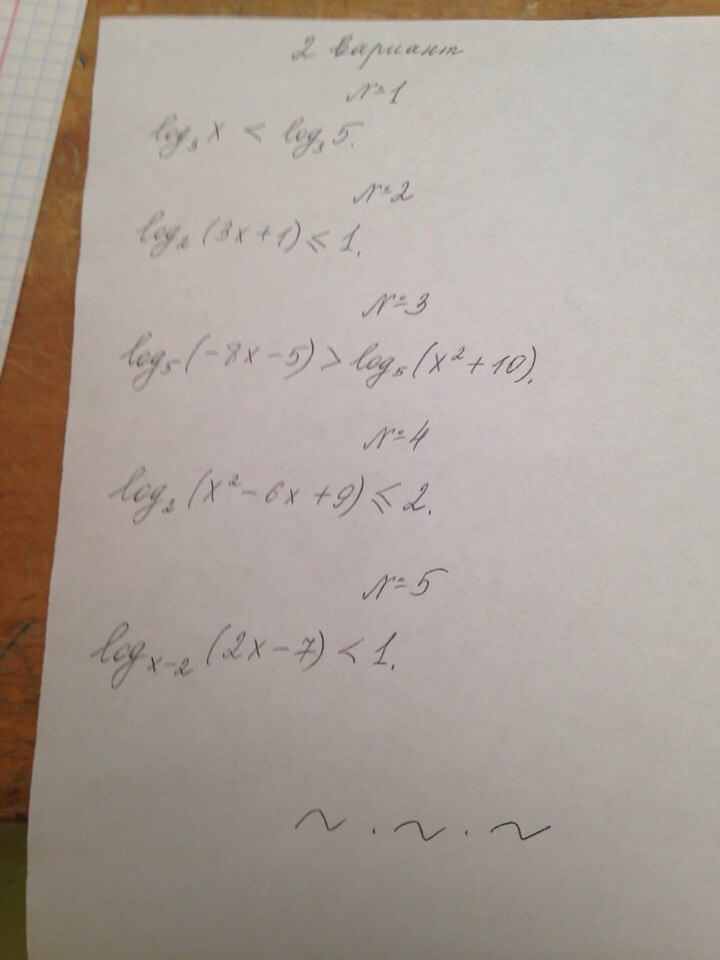
Ответы
Автор ответа:
0
Номер 4

Автор ответа:
0
Не забываем, что выражение под логарифмом должно быть больше нуля (здесь выполняется)
Автор ответа:
0
Так как 2 = log(2,4), то исходное неравенство можно записать так: log(2,(x²-6x+9) ≤ log(2,4).
Отсюда получаем x²-6x+9 ≤ 4 или x²-6x+5 ≤ 0. Это часть параболы ниже оси Ох.
Находим пределы: x²-6x+5 = 0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:D=(-6)^2-4*1*5=36-4*5=36-20=16;
Дискриминант больше 0, уравнение имеет 2 корня:x_1=(√16-(-6))/(2*1)=(4-(-6))/2=(4+6)/2=10/2=5;x_2=(-√16-(-6))/(2*1)=(-4-(-6))/2=(-4+6)/2=2/2=1.
Искомый промежуток значений х находится между 1 и 5. Но так как логарифмируемое выражение x²-6x+9 при х = 3 превращается в 0, то это значение выпадает из корней.
Ответ: 1 ≤ x < 3,
3 < x ≤ 5.
Отсюда получаем x²-6x+9 ≤ 4 или x²-6x+5 ≤ 0. Это часть параболы ниже оси Ох.
Находим пределы: x²-6x+5 = 0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:D=(-6)^2-4*1*5=36-4*5=36-20=16;
Дискриминант больше 0, уравнение имеет 2 корня:x_1=(√16-(-6))/(2*1)=(4-(-6))/2=(4+6)/2=10/2=5;x_2=(-√16-(-6))/(2*1)=(-4-(-6))/2=(-4+6)/2=2/2=1.
Искомый промежуток значений х находится между 1 и 5. Но так как логарифмируемое выражение x²-6x+9 при х = 3 превращается в 0, то это значение выпадает из корней.
Ответ: 1 ≤ x < 3,
3 < x ≤ 5.
Похожие вопросы
Предмет: Литература,
автор: kajfodzannina
Предмет: Математика,
автор: fluffy080cloud
Предмет: Английский язык,
автор: Naruto4560
Предмет: Алгебра,
автор: musa101010
Предмет: Математика,
автор: vevhsjwnh