Предмет: Алгебра,
автор: АнанимкаОК
Помогите решить,задание во вложении)Заранее спс)
Приложения:
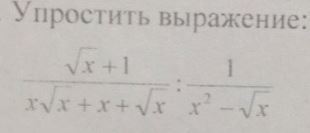
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: История,
автор: Аноним
Предмет: Литература,
автор: fustejilla97
Предмет: Другие предметы,
автор: daravolakova
Предмет: Математика,
автор: Adssgg
Предмет: Алгебра,
автор: Vikulka0017