Предмет: Математика,
автор: Аноним
помогите пожалуйста
Приложения:
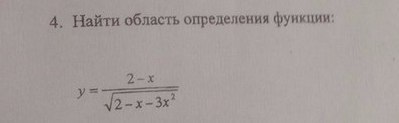
Ответы
Автор ответа:
0
ООФ выражение под корнем ≥0 по определению корня и ≠0 так как знаменатель ≠0, то есть >0
2-x-3x²>0 умножим на -1
3x²+x-2<0
решим неравенство методом интервалов
3x²+x-2=0, x1-2=(-1+-√1+24)/6=(-1+-5)/6={-1; 2/3)
1) при х<-1 например х=-2 3x²+x-2=12-2-2=-8 >0
2) при -1<х<2/3 например х=0 3x²+x-2=-2<0
3) при x>2/3 например х=1 3x²+x-2=1+1-2=2>0
выбираем тот интервал в котором 3х²+х-2<0
-1<x<2/3
или x∈(-1; 2/3)
2-x-3x²>0 умножим на -1
3x²+x-2<0
решим неравенство методом интервалов
3x²+x-2=0, x1-2=(-1+-√1+24)/6=(-1+-5)/6={-1; 2/3)
1) при х<-1 например х=-2 3x²+x-2=12-2-2=-8 >0
2) при -1<х<2/3 например х=0 3x²+x-2=-2<0
3) при x>2/3 например х=1 3x²+x-2=1+1-2=2>0
выбираем тот интервал в котором 3х²+х-2<0
-1<x<2/3
или x∈(-1; 2/3)
Похожие вопросы