Предмет: Алгебра,
автор: YALO001
!!!!!!!!!!!!Предел функции! за решение 30 пунктов!!!!!!!!!!!!!!
Приложения:

Ответы
Автор ответа:
0
Автор ответа:
0
мой вариант решения во вложении
Приложения:
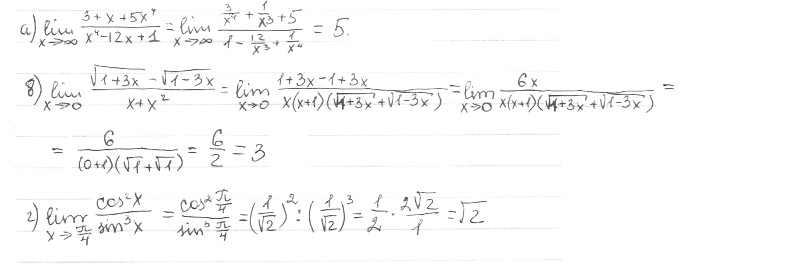
Похожие вопросы
Предмет: Английский язык,
автор: karisha68
Предмет: Русский язык,
автор: optimistdesgan
Предмет: Английский язык,
автор: samsung070168
Предмет: История,
автор: polinka1599