Предмет: Математика,
автор: Lено4кА
помогите,пожалуйста,решить производную)
Приложения:
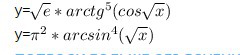
Ответы
Автор ответа:
0
это производные сложной функции y(g(x))=y'(g)*g'(x)
1) y'=(√e)(4arctg(cos√x)^4)*(arctg(cos√x))'=5(√e)[(arctg(cos√x))^4]***{1/(1+cos²√x}*(cos√x)'=5(√e)[(arctg(cos√x))^4]*{1/(1+cos²(√x)}*(-sin√x)*(√x)'=
=-5(√e)[(arctg(cos√x))^4](sin√x)*1/{(2√x)*(1+cos²√x))=-(5/2)(√e)*[(arctg(√x))^4]*(sin√x)/{√x/(1+cos²√x)}
2) y'=π²*(4arcsin³(√x))*(arcsin√x)'=4π²(arcsin³(√x))[1/√(1-x)](√x)'=4π²(arcsin³(√x))[1/√(1-x)](1/2√x)=2π²(arcsin³(√x))/{(1-x)√x}
1) y'=(√e)(4arctg(cos√x)^4)*(arctg(cos√x))'=5(√e)[(arctg(cos√x))^4]***{1/(1+cos²√x}*(cos√x)'=5(√e)[(arctg(cos√x))^4]*{1/(1+cos²(√x)}*(-sin√x)*(√x)'=
=-5(√e)[(arctg(cos√x))^4](sin√x)*1/{(2√x)*(1+cos²√x))=-(5/2)(√e)*[(arctg(√x))^4]*(sin√x)/{√x/(1+cos²√x)}
2) y'=π²*(4arcsin³(√x))*(arcsin√x)'=4π²(arcsin³(√x))[1/√(1-x)](√x)'=4π²(arcsin³(√x))[1/√(1-x)](1/2√x)=2π²(arcsin³(√x))/{(1-x)√x}
Похожие вопросы
Предмет: Физика,
автор: DIMAHEHE
Предмет: Английский язык,
автор: AiganymGanieva
Предмет: Биология,
автор: Crokyyyyysss
Предмет: Физика,
автор: alenschicler