Предмет: Геометрия,
автор: ludo4ka438
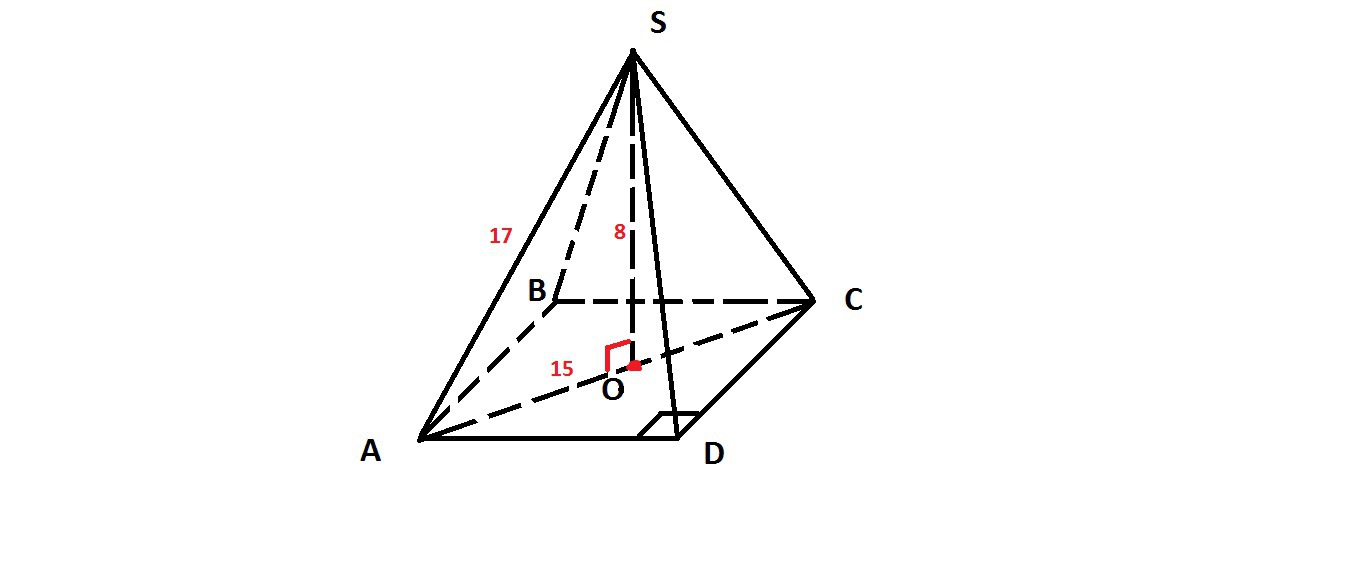
в правильной четырехугольной пирамиде SABCD точка О - центр основания, S вершина, SO=8см,SA=17см. Найди длину отрезка AC
Ответы
Автор ответа:
0
OA = 15
AC = 2OA = 30
Автор ответа:
0
Если пирамида правильная, то высота этой пирамиды проходит через центр основания. То есть SO-высота, значит ∠SOA=90°
AO²=AS²-SO²=17²-8²=225
AO=√225=15
Центром ПРАВИЛЬНОГО МНОГОУГОЛЬНИКА называется цент вписанной и описанной окружностей вокруг этого многоугольника, следовательно АО=ОС - как радиусы описанной окружности
АС=2АО=2*15=30
отв:30
AO²=AS²-SO²=17²-8²=225
AO=√225=15
Центром ПРАВИЛЬНОГО МНОГОУГОЛЬНИКА называется цент вписанной и описанной окружностей вокруг этого многоугольника, следовательно АО=ОС - как радиусы описанной окружности
АС=2АО=2*15=30
отв:30
Приложения:
Похожие вопросы
Предмет: Химия,
автор: dimascharuk2005
Предмет: История,
автор: zaipra54
Предмет: История,
автор: lsussnvshs
Предмет: Математика,
автор: Аноним
Предмет: Геометрия,
автор: акмарал75